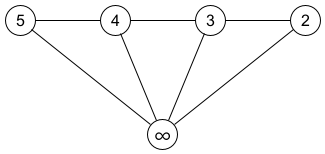
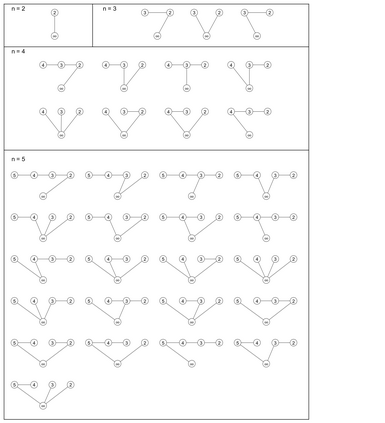
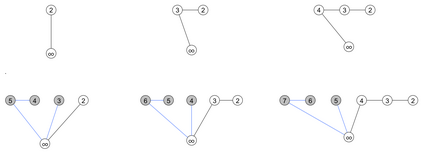
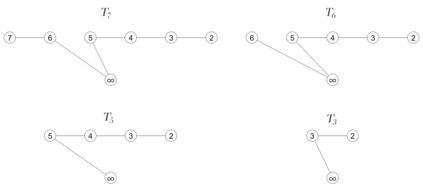
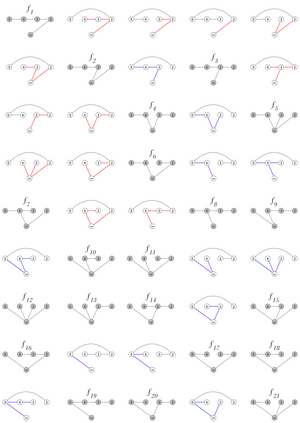
We consider the problem of listing all spanning trees of a graph $G$ such that successive trees differ by pivoting a single edge around a vertex. Such a listing is called a "pivot Gray code", and it has more stringent conditions than known "revolving-door" Gray codes for spanning trees. Most revolving-door algorithms employ a standard edge-deletion/edge-contraction recursive approach which we demonstrate presents natural challenges when requiring the "pivot" property. Our main result is the discovery of a greedy strategy to list the spanning trees of the fan graph in a pivot Gray code order. It is the first greedy algorithm for exhaustively generating spanning trees using such a minimal change operation. The resulting listing is then studied to find a recursive algorithm that produces the same listing in $O(1)$-amortized time using $O(n)$ space. Additionally, we present $O(n)$-time algorithms for ranking and unranking the spanning trees for our listing; an improvement over the generic $O(n^3)$-time algorithm for ranking and unranking spanning trees of an arbitrary graph. Finally, we discuss how our listing can be applied to find a pivot Gray code for the wheel graph.
翻译:我们考虑的是将所有横贯的树都列入一个图形$G$的问题,这样一连串的树木会因在顶层周围加注一个边缘而出现差异。这样的列表被称为“浮雕灰色代码 ”, 其条件比已知的“ 旋转门” 灰色代码” 更严格。 大多数旋转门算法使用标准的边缘删除/ 边缘合同递合法, 在要求“ 浮雕” 属性时, 我们展示了这种方法的自然挑战。 我们的主要结果是发现一种贪婪的战略, 将风扇图的树木排入一个浮雕刻在一条灰色代码的顺序中。 这是使用这种最小的改变操作来全面生成树的首个贪婪算法 。 然后对由此得出的列表进行了研究, 以找到一种重复式的算法, 用$(n) 空间来生成相同的边际删除列表 。 此外, 我们用$(n) $(n)- time 算出时间算法来排列和不排列我们的列表; 改进了通用的 $(n) $(n3)- time) 时间算方法, 用于讨论如何将树排成一个任意的图表。