Gaussian Mask Convolution for Convolutional Neural Networks

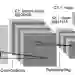
Square convolution is a default unit in convolutional neural networks as it fits well on the tensor computation for convolution operation, which usually has a fixed N x N receptive field (RF). However, what matters most to the network is the effective receptive field (ERF), which indicates the extent each pixel contributes to the output. ERF shows a Gaussian distribution and can not be modeled by simply sampling pixels with offsets. To simulate ERF, we propose a Gaussian Mask convolutional kernel (GMConv) in this work. Specifically, GMConv utilizes the Gaussian function to generate a concentric symmetry mask and put the mask over the kernel to refine the RF. Our GMConv can directly replace the standard convolutions in existing CNNs and can be easily trained end-to-end by standard backpropagation. Extensive experiments on multiple image classification benchmark datasets show that our method is comparable to, and outperforms in many cases, the standard convolution. For instance, using GMConv for AlexNet and ResNet-50, the top-1 accuracy on ImageNet classification is boosted by 0.98% and 0.85%, respectively.