Deep neural networks can stably solve high-dimensional, noisy, non-linear inverse problems

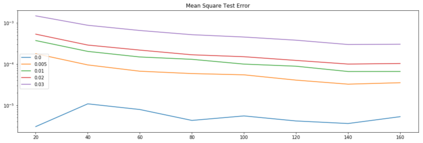
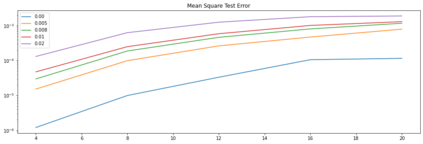
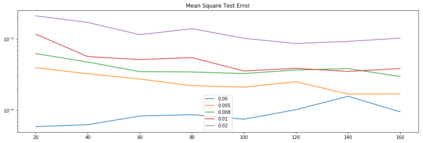
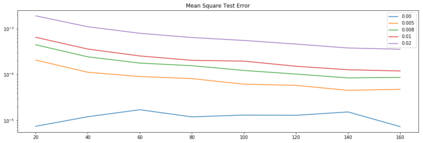
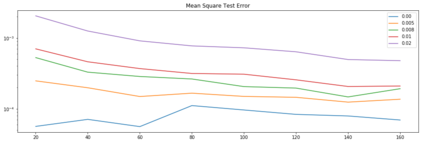
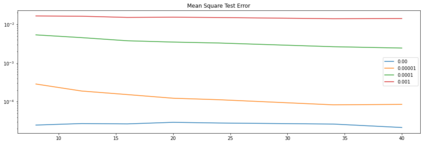
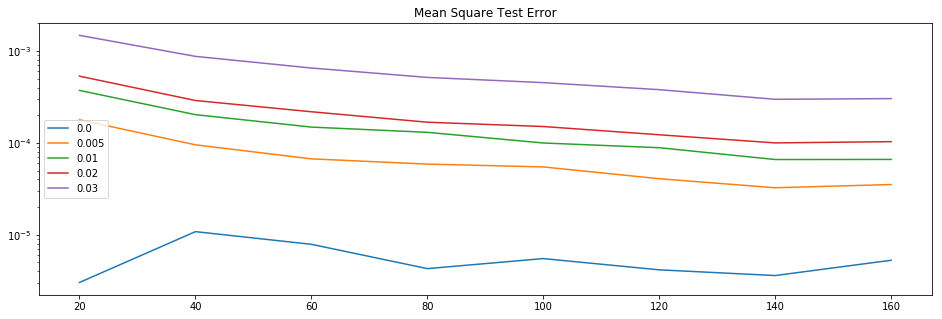
We study the problem of reconstructing solutions of inverse problems with neural networks when only noisy data is available. We assume the problem can be modeled with an infinite-dimensional forward operator that is not continuously invertible. Then, we restrict this forward operator to finite-dimensional spaces so that the inverse is Lipschitz continuous. For the inverse operator, we demonstrate that there exists a neural network which is a robust-to-noise approximation of the function. In addition, we show that these neural networks can be learned from appropriately perturbed training data. We demonstrate the admissibility of this approach to a wide range of inverse problems of practical interest. Numerical examples are given that support the theoretical findings.