Transitions from P to NP-hardness: the case of the Linear Ordering Problem

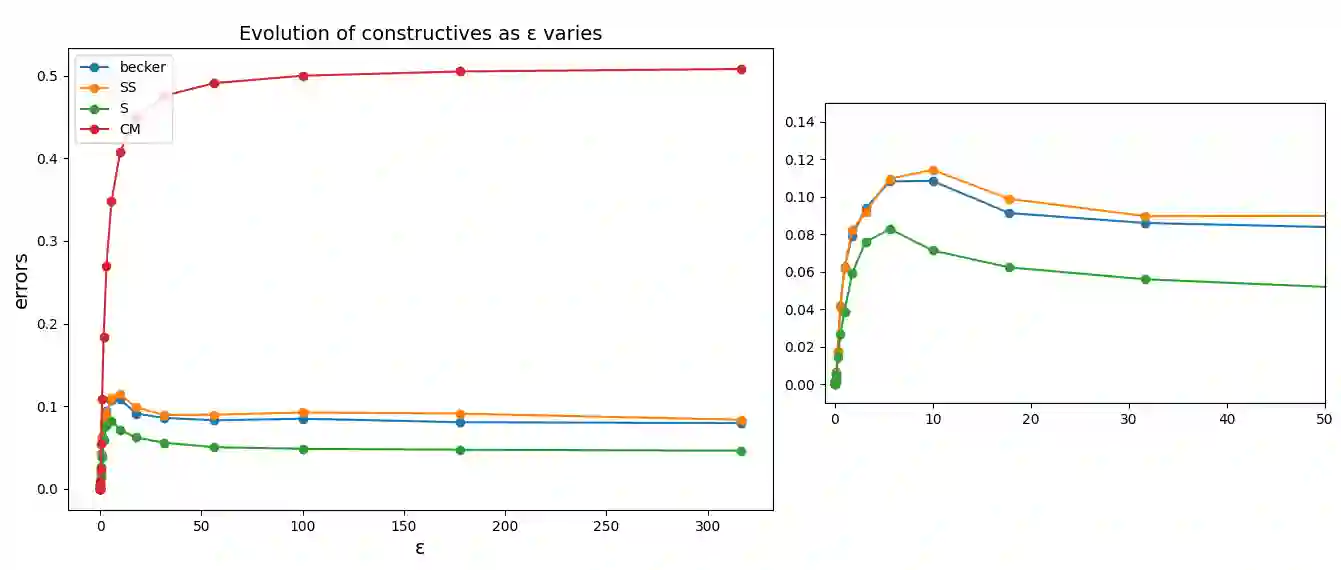
In this paper we evaluate how constructive heuristics degrade when a problem transits from P to NP-hard. This is done by means of the linear ordering problem. More specifically, for this problem we prove that the objective function can be expressed as the sum of two objective functions, one of which is associated with a P problem (an exact polynomial time algorithm is proposed to solve it), while the other is associated with an NP-hard problem. We study how different constructive algorithms whose behaviour only depends on univariate information perform depending on the contribution of the P or NP-hard components of the problem. A number of experiments are conducted with reduced dimensions, where the global optimum of the problems is known, giving different weights to the NP-hard component, while the weight of the P component is fixed. It is observed how the performance of the constructive algorithms gets worse as the weight given to the NP-hard component increases.