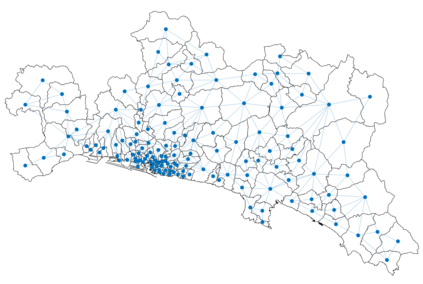
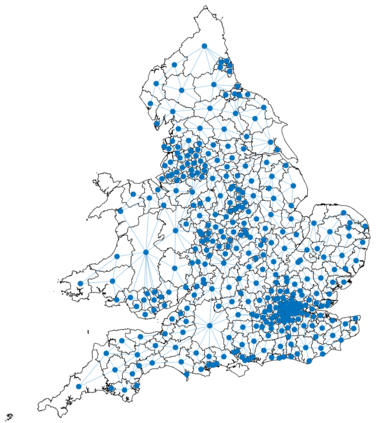
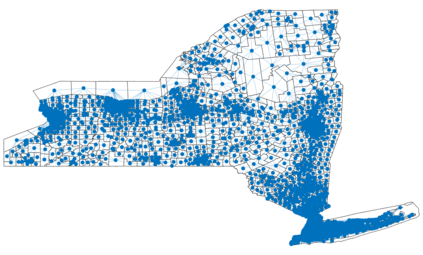
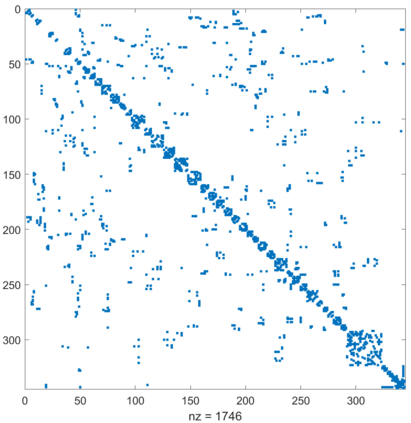
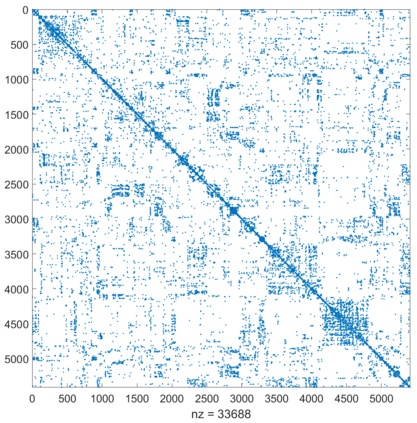
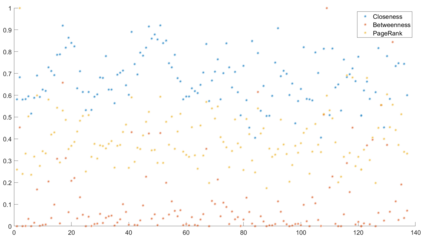
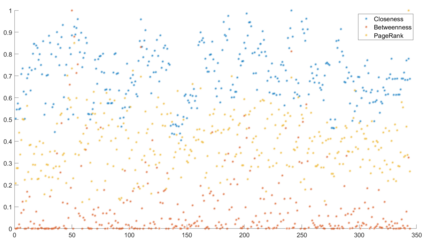
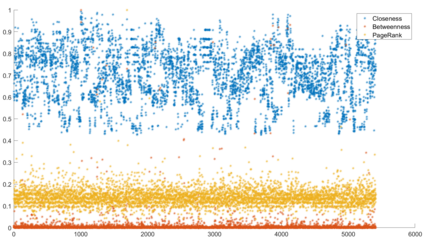
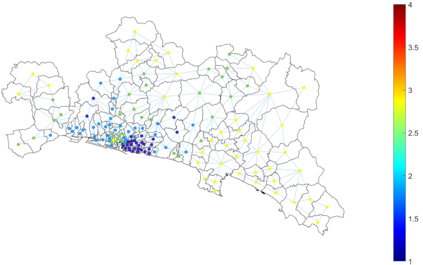
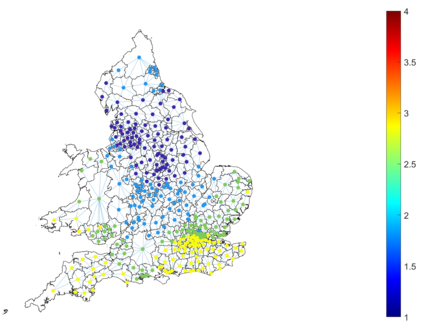
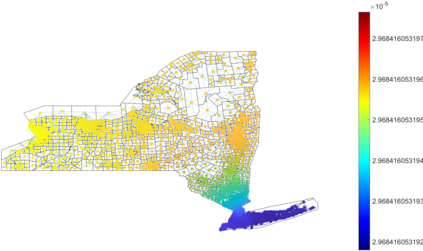
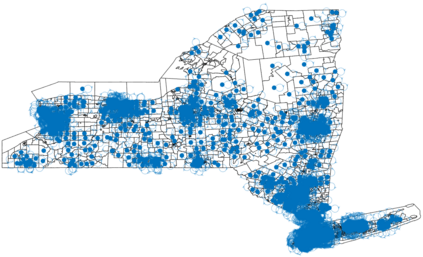
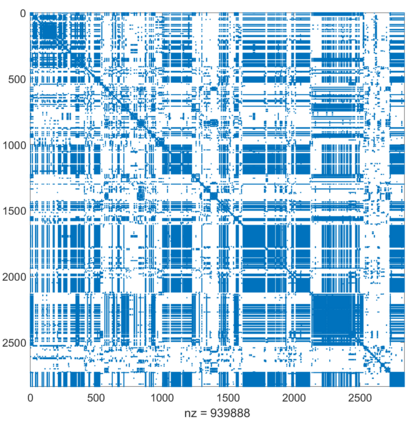
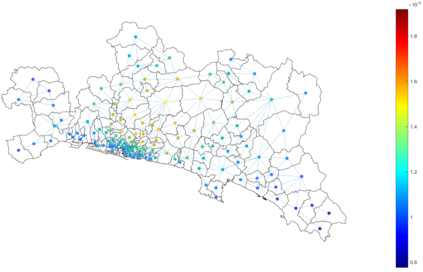
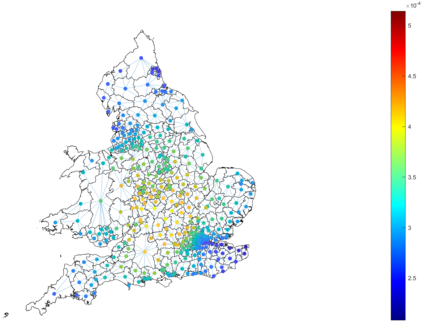
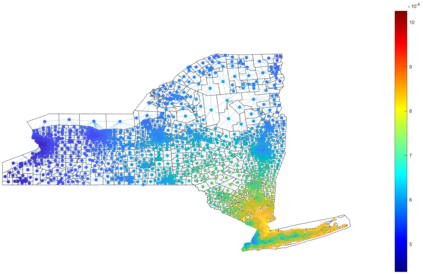
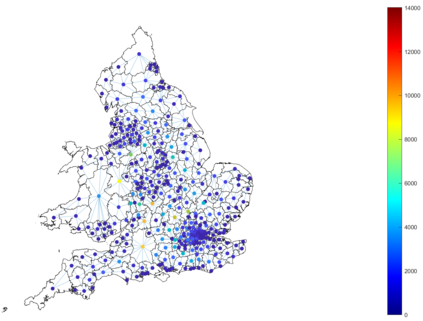
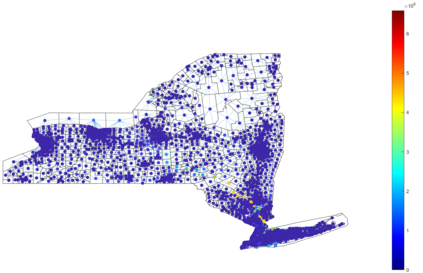
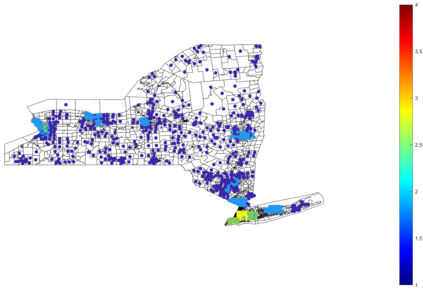
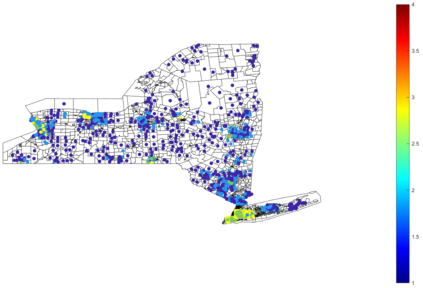
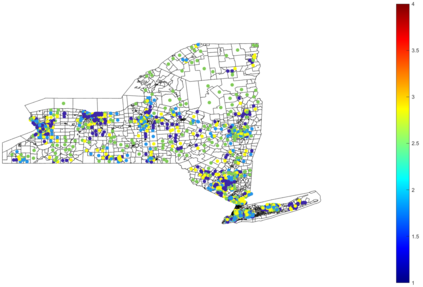
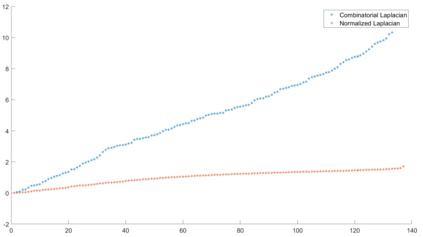
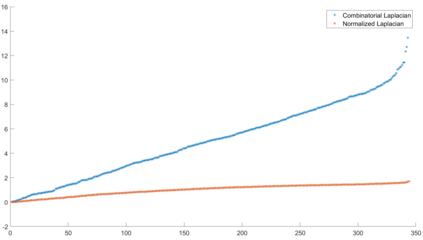
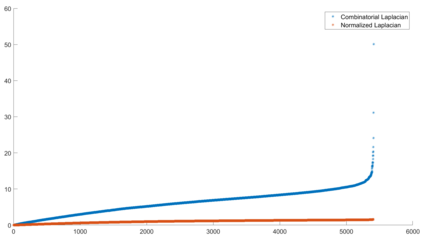
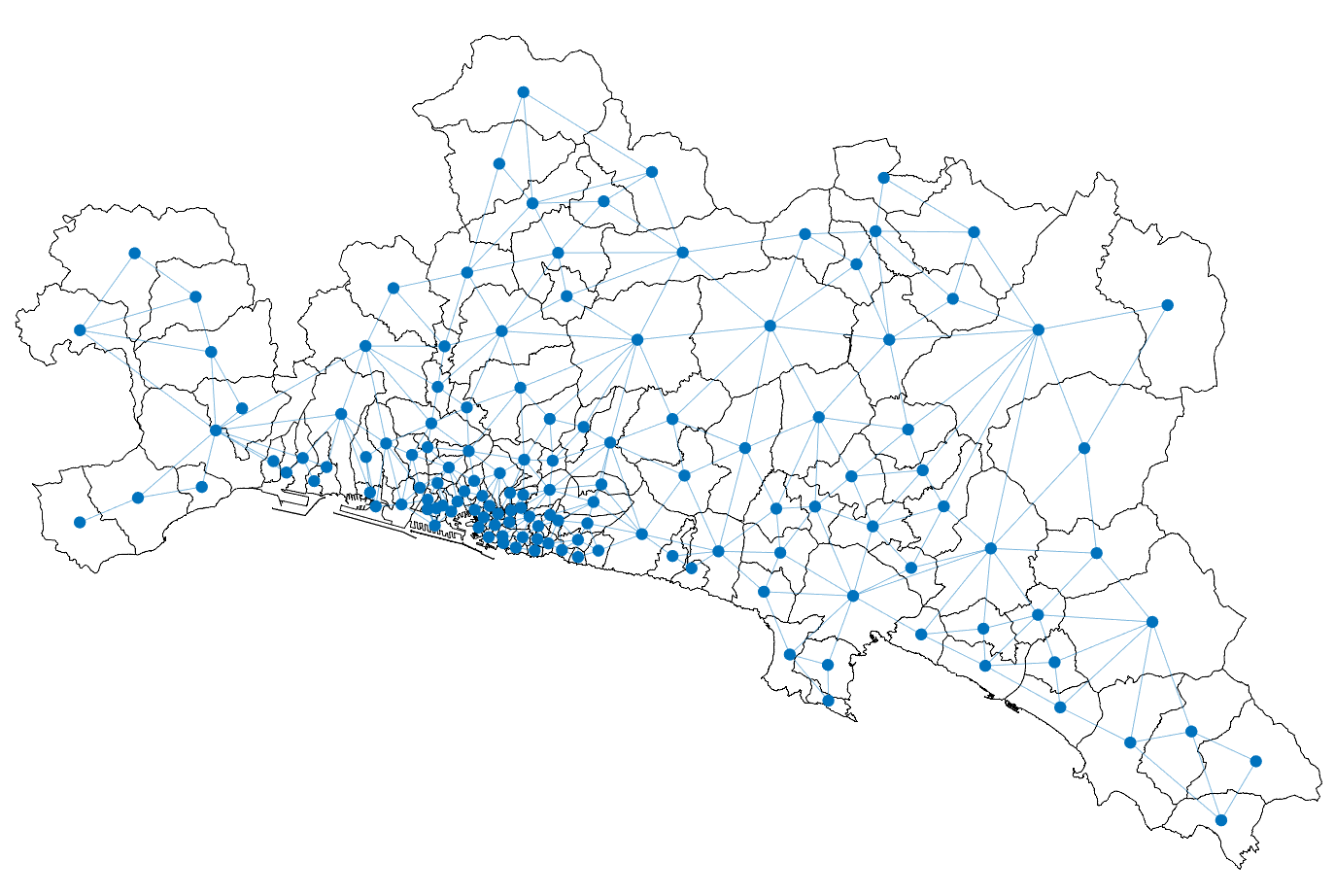
Urban mobility forecast and analysis can be addressed through grid-based and graph-based models. However, graph-based representations have the advantage of more realistically depicting the mobility networks and being more robust since they allow the implementation of Graph Theory machinery, enhancing the analysis and visualisation of mobility flows. We define two types of mobility graphs: Region Adjacency graphs and Origin-Destination graphs. Several node centrality metrics of graphs are applied to identify the most relevant nodes of the network in terms of graph connectivity. Additionally, the Perron vector associated with a strongly connected graph is applied to define a circulation function on the mobility graph. Such node values are visualised in the geographically embedded graphs, showing clustering patterns within the network. Since mobility graphs can be directed or undirected, we define several Graph Laplacian for both cases and show that these matrices and their spectral properties provide insightful information for network analysis. The computation of node centrality metrics and Perron-induced circulation functions for three different geographical regions demonstrate that basic elements from Graph Theory applied to mobility networks can lead to structure analysis for graphs of different connectivity, size, and orientation properties.
翻译:暂无翻译