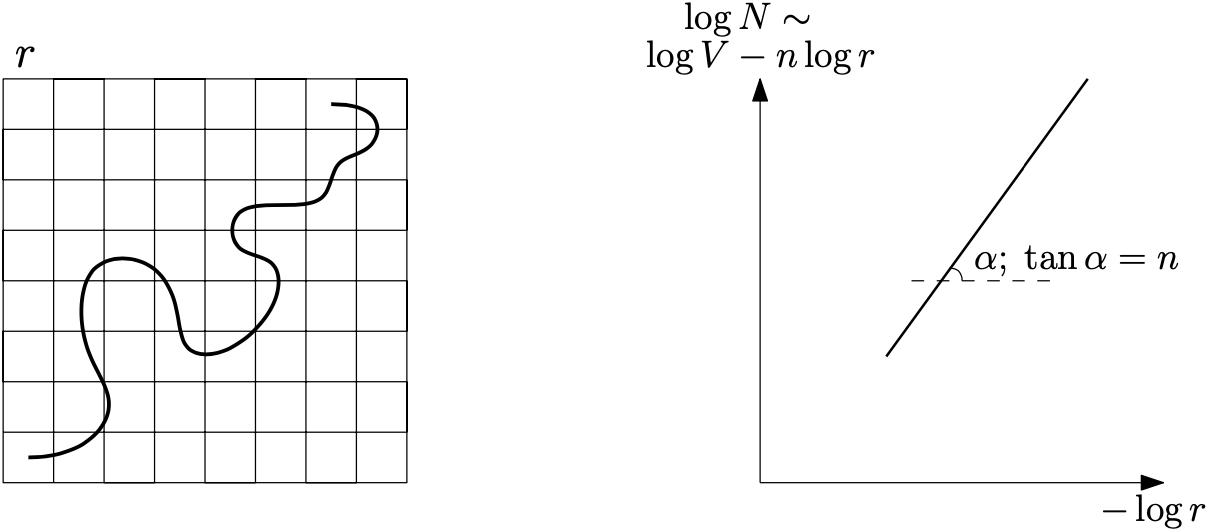
Manifold hypothesis states that data points in high-dimensional space actually lie in close vicinity of a manifold of much lower dimension. In many cases this hypothesis was empirically verified and used to enhance unsupervised and semi-supervised learning. Here we present new approach to manifold hypothesis checking and underlying manifold dimension estimation. In order to do it we use two very different methods simultaneously - one geometric, another probabilistic - and check whether they give the same result. Our geometrical method is a modification for sparse data of a well-known box-counting algorithm for Minkowski dimension calculation. The probabilistic method is new. Although it exploits standard nearest neighborhood distance, it is different from methods which were previously used in such situations. This method is robust, fast and includes special preliminary data transformation. Experiments on real datasets show that the suggested approach based on two methods combination is powerful and effective.
翻译:曼化假设指出,在高维空间的数据点实际上与多维的多维相近。 在很多情况下,这一假设是经过经验验证的,并用来加强未经监督和半监督的学习。 我们在这里提出了多重假设检查和基本多维估计的新方法。 为了做到这一点,我们同时使用两种截然不同的方法 — — 一个几何,另一个概率 — 并检查它们是否得出相同的结果。我们的几何方法是修改明考斯基维度计算众所周知的箱式计算算法的稀疏数据。 概率法是新的。 虽然它利用了标准的近邻距离,但它与以前在这类情况下使用的方法不同。 这种方法是稳健的, 快速的, 包括特殊的初步数据转换。 对真实数据集的实验表明,基于两种方法组合的建议方法的方法是有力和有效的。