Two-phase geothermal model with fracture network and multi-branch wells

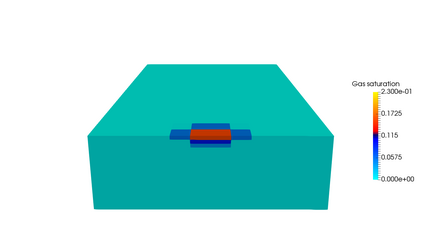
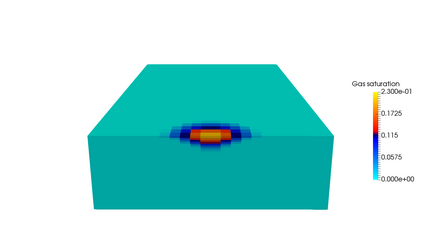
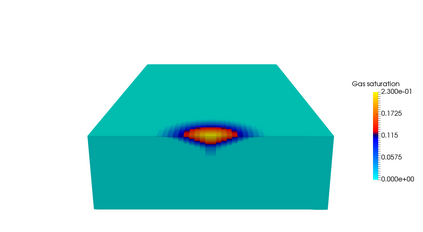
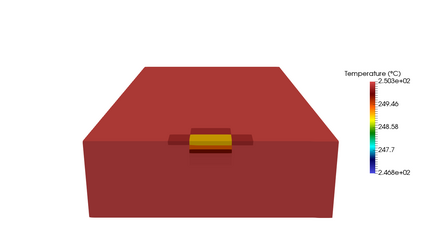
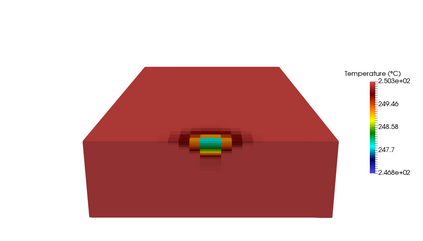
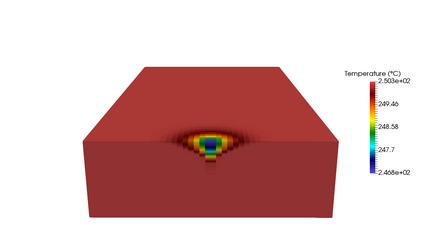
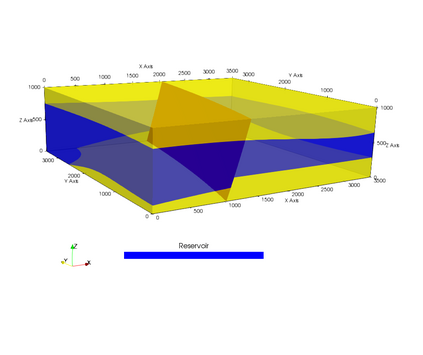
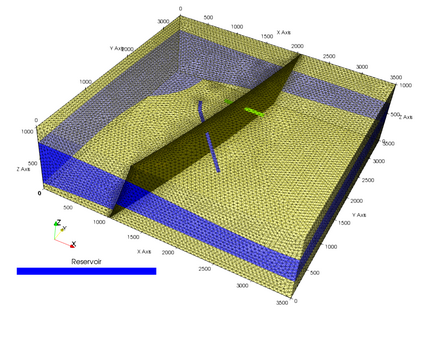
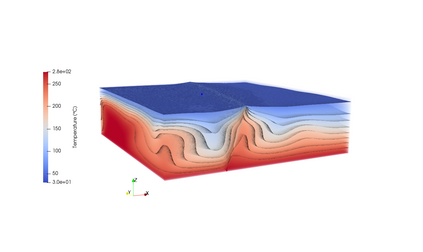
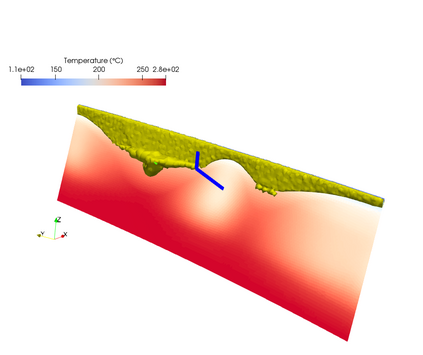
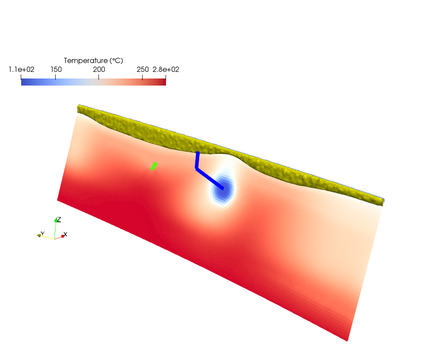
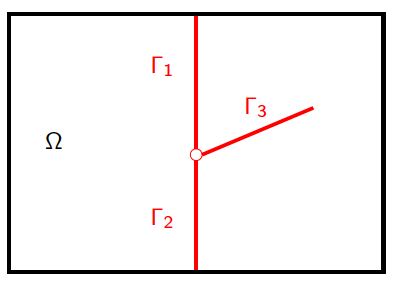
This paper focuses on the numerical simulation of geothermal systems in complex geological settings. The physical model is based on two-phase Darcy flows coupling the mass conservation of the water component with the energy conservation and the liquid vapor thermodynamical equilibrium. The discretization exploits the flexibility of unstructured meshes to model complex geology including conductive faults as well as complex wells. The polytopal and essentially nodal Vertex Approximate Gradient scheme is used for the approximation of the Darcy and Fourier fluxes combined with a Control Volume approach for the transport of mass and energy. Particular attention is paid to the faults which are modelled as two-dimensional interfaces defined as collection of faces of the mesh and to the flow inside deviated or multi-branch wells defined as collection of edges of the mesh with rooted tree data structure. By using an explicit pressure drop calculation, the well model reduces to a single equation based on complementarity constraints with only one well implicit unknown. The coupled systems are solved fully implicitely at each time step using efficient nonlinear and linear solvers on parallel distributed architectures. The convergence of the discrete model is investigated numerically on a simple test case with a Cartesian geometry and a single vertical producer well. Then, the ability of our approach to deal efficiently with realistic test cases is assessed on a high energy faulted geothermal reservoir operated using a doublet of two deviated wells.