Bayesian Inference for Multivariate Monotone Densities

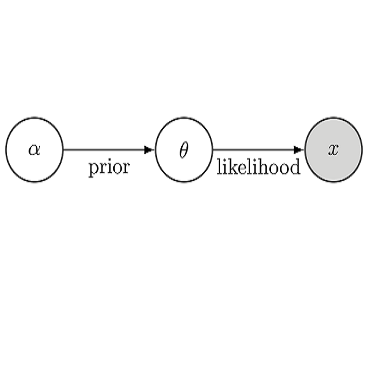
We consider a nonparametric Bayesian approach to estimation and testing for a multivariate monotone density. Instead of following the conventional Bayesian route of putting a prior distribution complying with the monotonicity restriction, we put a prior on the step heights through binning and a Dirichlet distribution. An arbitrary piece-wise constant probability density is converted to a monotone one by a projection map, taking its $\mathbb{L}_1$-projection onto the space of monotone functions, which is subsequently normalized to integrate to one. We construct consistent Bayesian tests to test multivariate monotonicity of a probability density based on the $\mathbb{L}_1$-distance to the class of monotone functions. The test is shown to have a size going to zero and high power against alternatives sufficiently separated from the null hypothesis. To obtain a Bayesian credible interval for the value of the density function at an interior point with guaranteed asymptotic frequentist coverage, we consider a posterior quantile interval of an induced map transforming the function value to its value optimized over certain blocks. The limiting coverage is explicitly calculated and is seen to be higher than the credibility level used in the construction. By exploring the asymptotic relationship between the coverage and the credibility, we show that a desired asymptomatic coverage can be obtained exactly by starting with an appropriate credibility level.