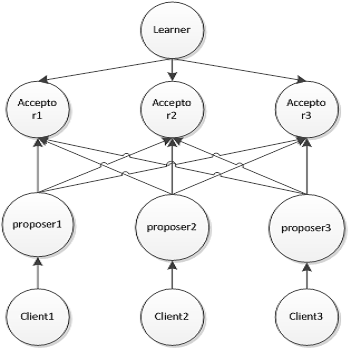
In distributed systems, a group of $\textit{learners}$ achieve $\textit{consensus}$ when, by observing the output of some $\textit{acceptors}$, they all arrive at the same value. Consensus is crucial for ordering transactions in failure-tolerant systems. Traditional consensus algorithms are homogeneous in three ways: - all learners are treated equally, - all acceptors are treated equally, and - all failures are treated equally. These assumptions, however, are unsuitable for cross-domain applications, including blockchains, where not all acceptors are equally trustworthy, and not all learners have the same assumptions and priorities. We present the first consensus algorithm to be heterogeneous in all three respects. Learners set their own mixed failure tolerances over differently trusted sets of acceptors. We express these assumptions in a novel $\textit{Learner Graph}$, and demonstrate sufficient conditions for consensus. We present $\textit{Heterogeneous Paxos}$: an extension of Byzantine Paxos. Heterogeneous Paxos achieves consensus for any viable Learner Graph in best-case three message sends, which is optimal. We present a proof-of-concept implementation, and demonstrate how tailoring for heterogeneous scenarios can save resources and latency.
翻译:在分布式系统中,一组美元(textit{learners}$)达到美元(textit{consensuus}$),而一组美元(textit{consens}$)通过观察某些美元(textit{接受者}$)的输出,它们都达到相同的价值。共识对于在不耐失的系统中订购交易至关重要。传统的协商一致算法在三种方式上是同质的:所有学习者都得到同等待遇,所有接受者都得到同等待遇,所有失败都得到同等待遇。然而,这些假设不适用于跨部应用,包括块链,其中并非所有接受者都同样值得信赖,并非所有学习者都有相同的假设和优先事项。我们提出了第一个共识算法,在所有三个方面都是异质的。学习者将自己的混合失败容忍度设置在不同的受信任的接受者组中。我们用新颖的美元(textitunit{Learner Graphat}表达这些假设,并展示足够的协商一致条件。我们提出了美元(Hetrogenouspecious pax) $:Byzantine Paxtous a a a sult-cent review of prespresmal laviolview) laview shing shing shing