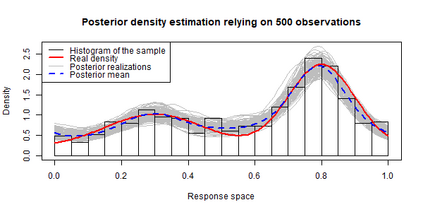
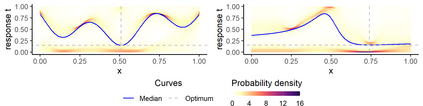
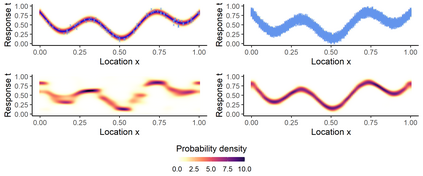
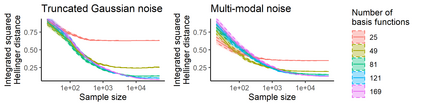
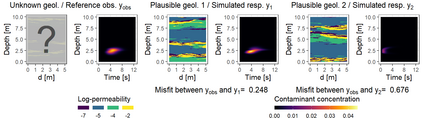
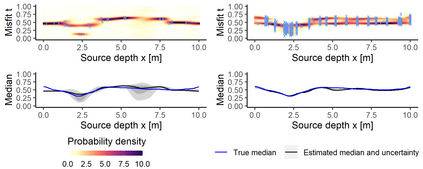
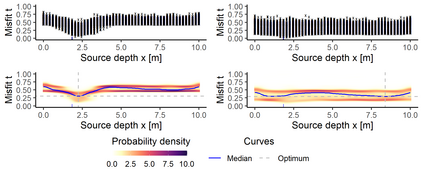
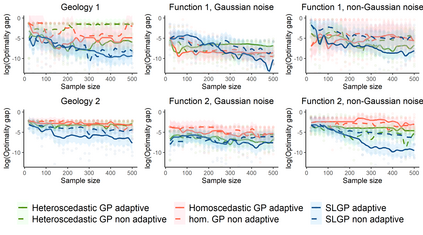
In the study of natural and artificial complex systems, responses that are not completely determined by the considered decision variables are commonly modelled probabilistically, resulting in response distributions varying across decision space. We consider cases where the spatial variation of these response distributions does not only concern their mean and/or variance but also other features including for instance shape or uni-modality versus multi-modality. Our contributions build upon a non-parametric Bayesian approach to modelling the thereby induced fields of probability distributions, and in particular to a spatial extension of the logistic Gaussian model. The considered models deliver probabilistic predictions of response distributions at candidate points, allowing for instance to perform (approximate) posterior simulations of probability density functions, to jointly predict multiple moments and other functionals of target distributions, as well as to quantify the impact of collecting new samples on the state of knowledge of the distribution field of interest. In particular, we introduce adaptive sampling strategies leveraging the potential of the considered random distribution field models to guide system evaluations in a goal-oriented way, with a view towards parsimoniously addressing calibration and related problems from non-linear (stochastic) inversion and global optimisation.
翻译:在对自然和人工复杂系统的研究中,未完全由所考虑的决定变量确定的反应通常是模拟概率的,结果在决定空间之间的反应分布不尽相同。我们考虑的是,这些反应分布的空间变化不仅涉及其平均值和/或差异,而且涉及其他特征,例如形状或单一时态相对于多时制等特征。我们的贡献基于一种非参数的巴伊西亚方法来模拟由此引发的概率分布领域,特别是后勤模式的空间扩展。这些经过考虑的模型对候选点的响应分布作出概率预测,允许对概率密度功能进行(近似)事后模拟,共同预测目标分布的多重时刻和其他功能,并量化收集新样品对利益分布领域知识状况的影响。我们特别采用适应性抽样战略,利用考虑随机分布的实地模型的潜力,以目标导向的方式指导系统评价,以便从不偏重校准和从选择转向全球选择(从选择到选择)和相关问题。