Asymptotic expansions of high-frequency multiple scattering iterations for sound hard scattering problems

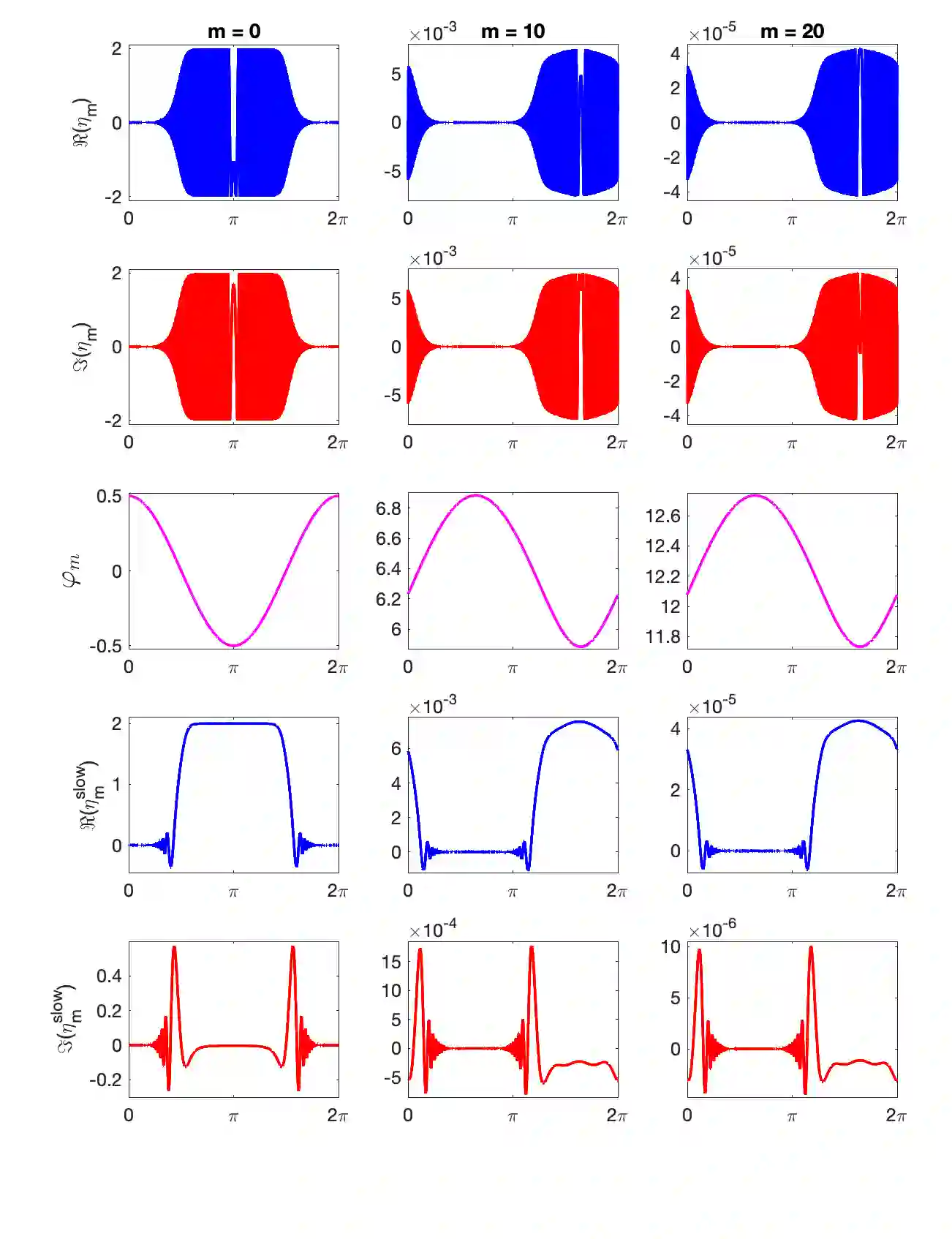
We consider the two-dimensional high-frequency plane wave scattering problem in the exterior of a finite collection of disjoint, compact, smooth, strictly convex obstacles with Neumann boundary conditions. Using integral equation formulations, we determine the H\"{o}rmander classes and derive high-frequency asymptotic expansions of the total fields corresponding to multiple scattering iterations on the boundaries of the scattering obstacles. These asymptotic expansions are used to obtain sharp wavenumber dependent estimates on the derivatives of multiple scattering total fields which, in turn, allow for the optimal design and numerical analysis of Galerkin boundary element methods for the efficient (frequency independent) approximation of sound hard multiple scattering returns. Numerical experiments supporting the validity of these expansions are presented.