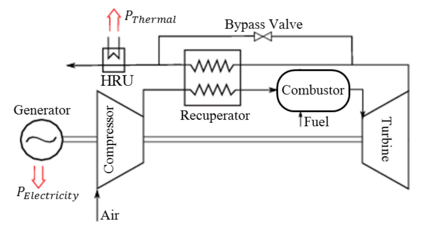
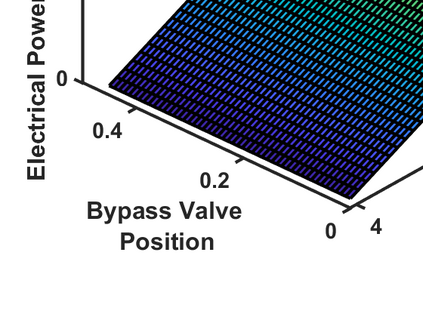
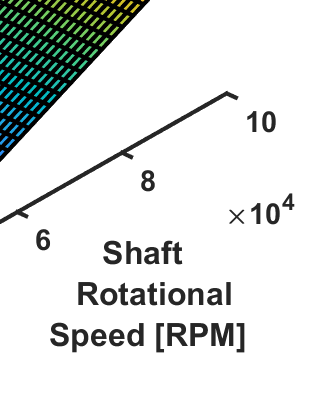
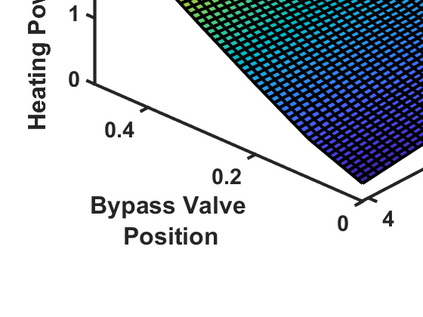
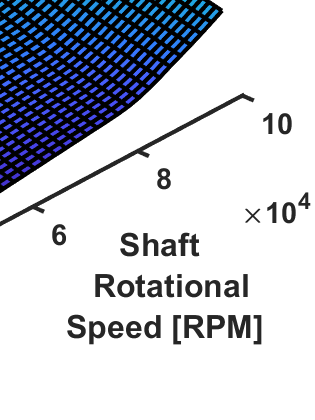
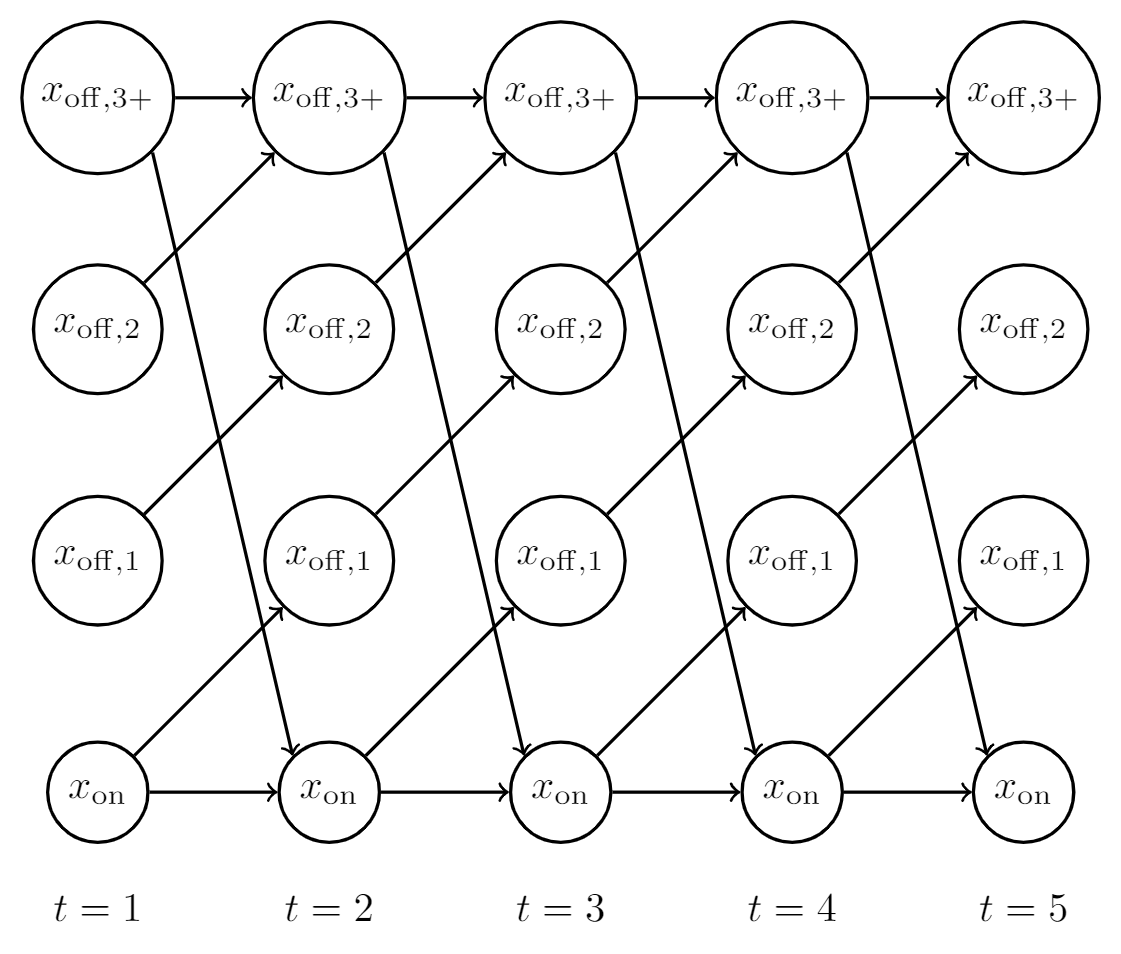
This work considers the economic dispatch problem for a single micro-gas turbine, governed by a discrete state-space model, under combined heat and power (CHP) operation and coupled with a utility. If the exact power and heat demands are given, existing algorithms can be used to give a quick optimal solution to the economic dispatch problem. However, in practice, the power and heat demands can not be known deterministically, but are rather predicted, resulting in an estimate and a bound on the estimation error. We consider the case in which the power and heat demands are unknown, and present a robust optimization-based approach for scheduling the turbine's heat and power generation, in which the demand is assumed to be inside an uncertainty set. We consider two different choices of the uncertainty set relying on the $\ell^\infty$- and the $\ell^1$-norms, each with different advantages, and consider the associated robust economic dispatch problems. We recast these as robust shortest-path problems on appropriately defined graphs. For the first choice, we provide an exact linear-time algorithm for the solution of the robust shortest-path problem, and for the second, we provide an exact quadratic-time algorithm and an approximate linear-time algorithm. The efficiency and usefulness of the algorithms are demonstrated using a detailed case study that employs real data on energy demand profiles and electricity tariffs.
翻译:这项工作考虑了单一微气涡轮机的经济发热问题,由离散状态-空间模型管理,在热电合用下运行,并配有公用事业。如果提供确切的电力和热需求,现有的算法可以用来迅速最佳地解决经济发热问题。然而,在实践中,电力和热需求不能被确定性地知道,而是被预测,从而导致估算和受估算错误的约束。我们考虑了电力和热需求未知的情况,并提出了一种强有力的优化方法,用于安排涡轮机的热电发电,假设其需求在不确定的一组之内。我们考虑两种不同的不确定性选择,即依赖$\ell ⁇ infty-和$\ell_1$-norm,每个都具有不同优势,并考虑相关的强劲的经济发电问题。我们在适当界定的图表中重新表述了这些问题的最短路径问题。我们提供了精确的线性时间算法,用于解决最短路径问题的解决方案,并假设需求在一套不确定的电路程和精确的电算法上,我们提供了一种精确的电量和精确的电算法。