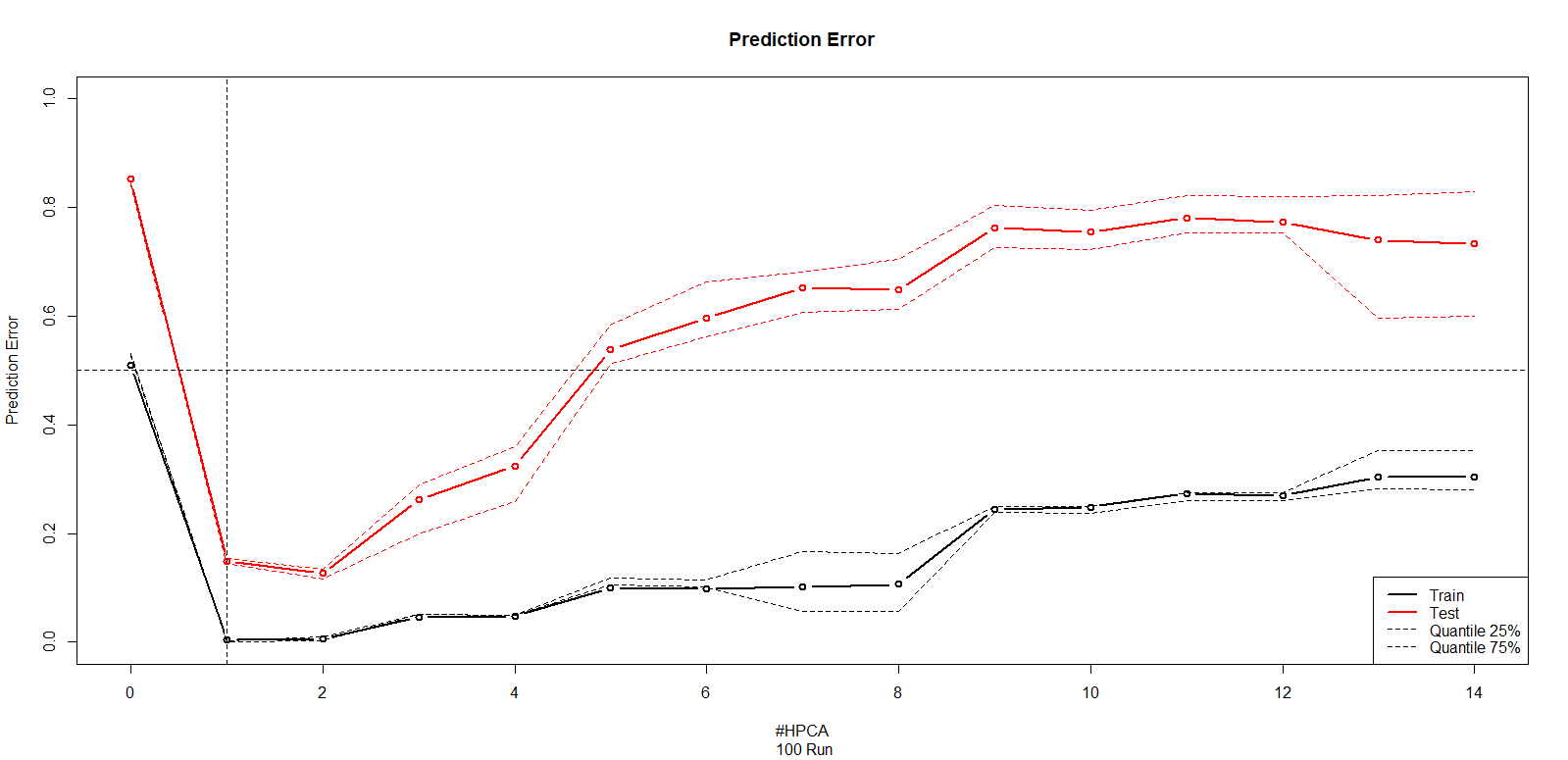
Objective: In some situations that exist both scalar and functional data, called mixed and hybrid data, the hybrid PCA (HPCA) was introduced. Among the regression models for the hybrid data, we can count covariate-adjusted HPCA, the Semi-functional partial linear regression, function-on-function (FOF) regression with signal compression, and functional additive regression, models. In this article, we study the effects of HPCA decomposition of hybrid data on the prediction accuracy of the FOF regression with signal compressions. Method: We stated a two-step procedure for incorporating the HPCA in the functional regressions. The first step is reconstructing the data based on the HPCAs and the second step is merging data on the other dimensions and calculate the point-wise average of the desired functional dimension. We also choose the number of HPCA based on Mean Squared Perdition Error (MSPE). Result: In the two simulations, we show that the regression models with the first HPCA have the best accuracy prediction and model fit summaries among no HPCA and all HPCAs with a training/testing approach. Finally, we applied our methodology to the EEG-fMRI dataset. Conclusions: We conclude that our methodology improves the prediction of the experiments with the EEG datasets. And we recommend that instead of using the functional PCA on the desired dimension, reconstruct the data with HPCA and average it on the other two dimensions for functional regression models.
翻译:目标: 在存在标度和功能性数据(称为混合和混合层面数据)的某些情况下,引入了混合五氯苯甲醚(HPCCA),在混合数据的回归模型中,我们可以计算共变调整的HPCA, 半功能部分线性回归, 功能上回归(FFOF), 信号压缩, 功能性添加回归(FOE) 模型。在本篇文章中,我们研究了HPCA对FO回归预测准确性和信号压缩的混合数据进行分解的影响。方法:我们指出将HPCA纳入功能回归的两步程序。第一步是重建基于HPCA的数据,第二步是合并其他维度的数据,计算预期功能性层面的点平均值。我们还根据中等偏差误差(MDE)选择HPCA的组合数据数量。结果:在两次模拟中,我们显示第一个HPCA和所有HPCA的回归模型具有最佳准确性预测和模型的精度。我们用培训/测试方法将HPCA的数据与ERC的功能性模型合并,最后我们用E-EA的预测方法,我们用E-E-E-BS的预测方法改进了E-A的数据。