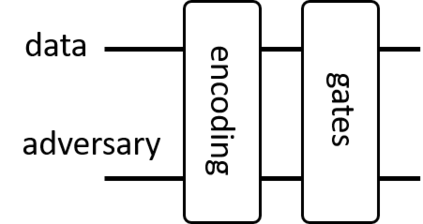
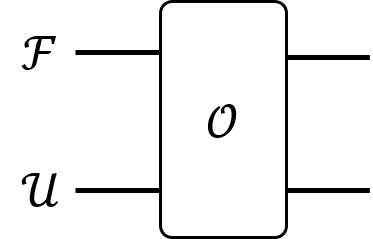
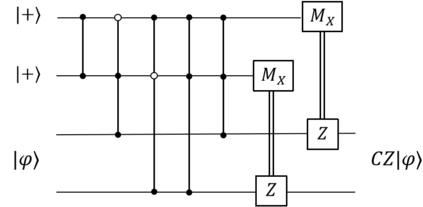
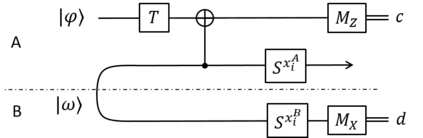
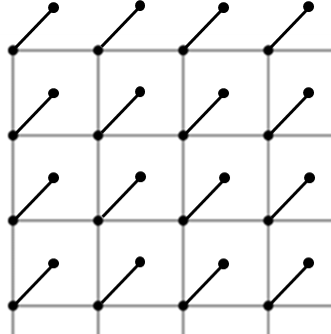
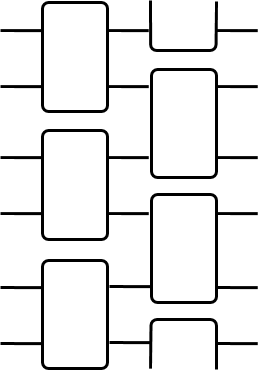
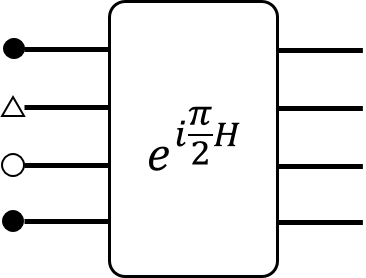
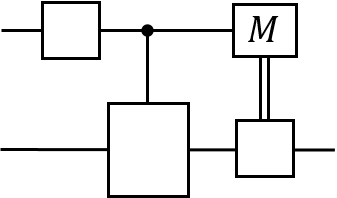Unravelling the source of quantum computing power has been a major goal in the field of quantum information science. In recent years, the quantum resource theory (QRT) has been established to characterize various quantum resources, yet their roles in quantum computing tasks still require investigation. The so-called universal quantum computing model (UQCM), e.g., the circuit model, has been the main framework to guide the design of quantum algorithms, creation of real quantum computers etc. In this work, we combine the study of UQCM together with QRT. We find on one hand, using QRT can provide a resource-theoretic characterization of a UQCM, the relation among models and inspire new ones, and on the other hand, using UQCM offers a framework to apply resources, study relation among resources and classify them. We develop the theory of universal resources in the setting of UQCM, and find a rich spectrum of UQCMs and the corresponding universal resources. Depending on a hierarchical structure of resource theories, we find models can be classified into families. In this work, we study three natural families of UQCMs in details: the amplitude family, the quasi-probability family, and the Hamiltonian family. They include some well known models, like the measurement-based model and adiabatic model, and also inspire new models such as the contextual model we introduce. Each family contains at least a triplet of models, and such a succinct structure of families of UQCMs offers a unifying picture to investigate resources and design models. It also provides a rigorous framework to resolve puzzles, such as the role of entanglement vs. interference, and unravel resource-theoretic features of quantum algorithms.
翻译:在数量信息科学领域,量化计算能力来源的模糊化一直是量子计算科学领域的一个主要目标。近年来,量子资源理论(QRT)的建立是为了确定各种量子资源的特点,但它们在量子计算任务中的作用仍需要调查。所谓的通用量子计算模型(UQCM),例如电路模型,一直是指导量子算法设计、创建真实量子计算机等的主要框架。在这项工作中,我们把对UQCM的研究与QRT的研究结合起来。我们发现,一方面,使用QRT可以提供UCM的资源理论描述,模型之间的关系和激励新的量子资源。另一方面,使用UQCMM提供了一个应用资源、研究资源关系和分类的框架。我们在UCMCM设置中开发了通用资源理论的理论,并发现了大量UQCMCM和相应的通用资源模型。根据资源理论的等级结构,我们发现可以将模型分解成家庭。在这项工作中,我们研究三个自然的量子家庭, 也就是所认识的量子、 家庭、 设计、 和等等等的模型。</s>