Random Algebraic Graphs and Their Convergence to Erdos-Renyi

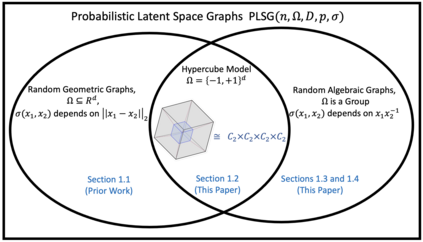
A random algebraic graph is defined by a group ${G}$ with a "uniform" distribution over it and a connection $\sigma:{G}\longrightarrow [0,1]$ with expectation $p,$ satisfying $\sigma({g}) = \sigma({g}^{-1}).$ The random graph $\mathsf{RAG}(n,{G},p,\sigma)$ with vertex set $[n]$ is formed as follows. First, $n$ independent latent vectors ${x}_1, \ldots, {x}_n$ are sampled uniformly from ${G}.$ Then, vertices $i,j$ are connected with probability $\sigma({x}_i{x}_j^{-1}).$ This model captures random geometric graphs with latent space the unit sphere and the hypercube, certain regimes of the stochastic block model, and random subgraphs of Cayley graphs. The main question of interest to the current paper is: when is a random algebraic graph statistically and/or computationally distinguishable from $\mathsf{G}(n,p)$? Our results fall into two main categories. 1) Geometric. We focus on the case ${G} =\{\pm1\}^d$ and use Fourier-analytic tools. For hard threshold connections, we match [LMSY22b] for $p = \omega(1/n)$ and for connections that are $\frac{1}{r\sqrt{d}}$-Lipschitz we extend the results of [LR21b] when $d = \Omega(n\log n)$ to the non-monotone setting. 2) Algebraic. We provide evidence for an exponential statistical-computational gap. Consider any finite group ${G}$ and let $A\subseteq {G}$ be a set of elements formed by including each set of the form $\{{g}, {g}^{-1}\}$ independently with probability $1/2.$ Let $\Gamma_n({G},A)$ be the distribution of random graphs formed by taking a uniformly random induced subgraph of size $n$ of the Cayley graph $\Gamma({G},A).$ Then, $\Gamma_n({G}, A)$ and $\mathsf{G}(n,1/2)$ are statistically indistinguishable with high probability over $A$ if and only if $\log |{G}| \gtrsim n.$ However, low-degree polynomial tests fail to distinguish $\Gamma_n({G}, A)$ and $\mathsf{G}(n,1/2)$ with high probability over $A$ when $\log |{G}| = \log^{\Omega(1)}n.$