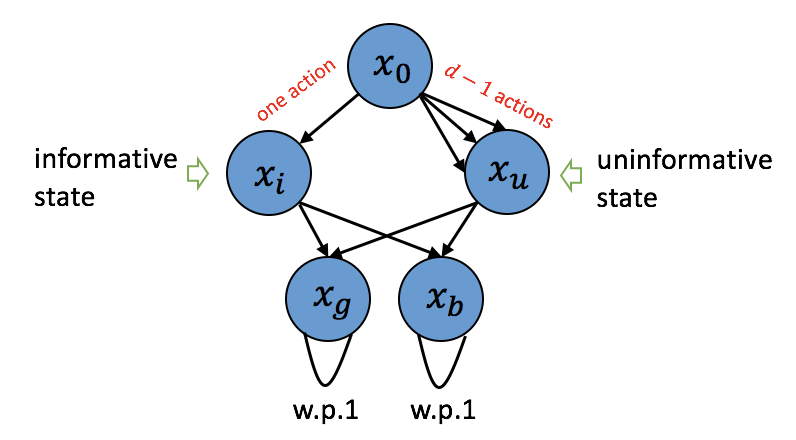
We investigate the hardness of online reinforcement learning in fixed horizon, sparse linear Markov decision process (MDP), with a special focus on the high-dimensional regime where the ambient dimension is larger than the number of episodes. Our contribution is two-fold. First, we provide a lower bound showing that linear regret is generally unavoidable in this case, even if there exists a policy that collects well-conditioned data. The lower bound construction uses an MDP with a fixed number of states while the number of actions scales with the ambient dimension. Note that when the horizon is fixed to one, the case of linear stochastic bandits, the linear regret can be avoided. Second, we show that if the learner has oracle access to a policy that collects well-conditioned data then a variant of Lasso fitted Q-iteration enjoys a nearly dimension-free regret of $\tilde{O}( s^{2/3} N^{2/3})$ where $N$ is the number of episodes and $s$ is the sparsity level. This shows that in the large-action setting, the difficulty of learning can be attributed to the difficulty of finding a good exploratory policy.
翻译:我们调查了在固定的地平线上进行在线强化学习的难度,即线性马尔科夫决定程序(MDP),特别侧重于环境层面大于事件数量的高维系统。 我们的贡献是双重的。 首先,我们提供了一个较低的约束,表明线性遗憾在本案中一般是不可避免的,即使存在收集良好数据的政策。 下约束的建筑使用一个具有固定数目的国家的MDP,而带有环境层面的行动尺度的数量是固定的。 请注意,当地平线被固定在一个区域时,线性随机强盗的情况可以避免线性遗憾。 其次,我们表明,如果学习者有机会接触一个收集良好数据的政策,那么一个适合Qiteration的Lasso变异体则几乎没有维度的遗憾, $tilde{O}( s ⁇ 2/3} N ⁇ 2/3} 美元, 其中美元是事件的数量, $sersity is the scorrisity level) 。 这表明,在大型行动环境中,学习的困难可以归因于寻找一个良好的探索政策的困难。