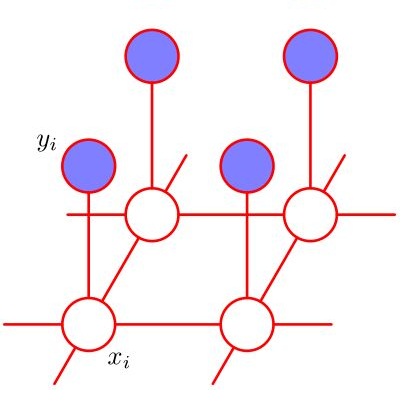
We propose risk models for a portfolio of risks, each following a compound Poisson distribution, with dependencies introduced through a family of tree-based Markov random fields with Poisson marginal distributions inspired in C\^ot\'e et al. (2024b, arXiv:2408.13649). The diversity of tree topologies allows for the construction of risk models under several dependence schemes. We study the distribution of the random vector of risks and of the aggregate claim amount of the portfolio. We perform two risk management tasks: the assessment of the global risk of the portfolio and its allocation to each component. Numerical examples illustrate the findings and the efficiency of the computation methods developed throughout. We also show that the discussed family of Markov random fields is a subfamily of the multivariate Poisson distribution constructed through common shocks.
翻译:暂无翻译