Optimal Stopping Theory for a Distributionally Robust Seller

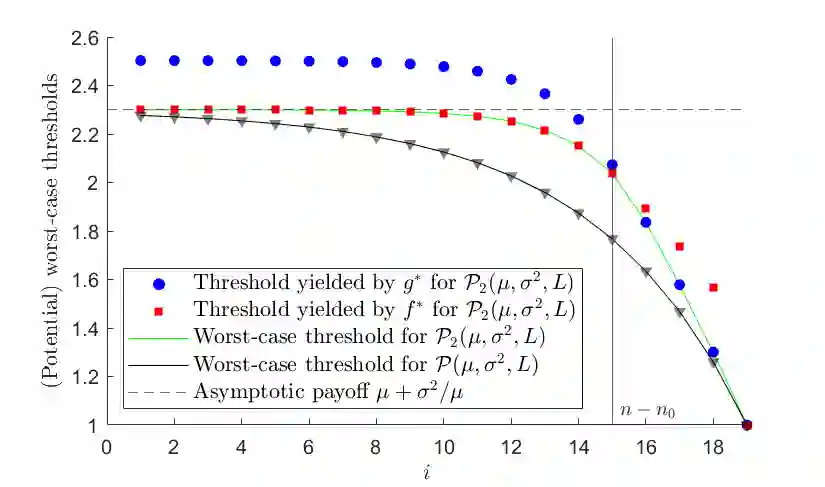
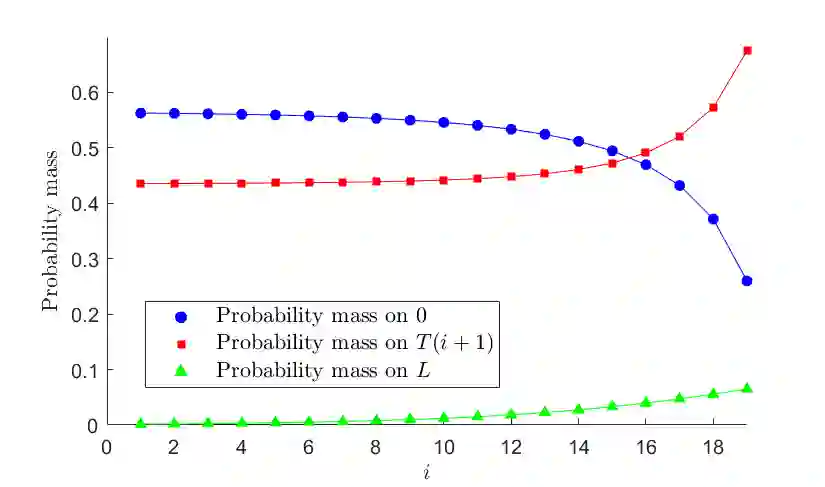
Sellers in online markets face the challenge of determining the right time to sell in view of uncertain future offers. Classical stopping theory assumes that sellers have full knowledge of the value distributions, and leverage this knowledge to determine stopping rules that maximize expected welfare. In practice, however, stopping rules must often be determined under partial information, based on scarce data or expert predictions. Consider a seller that has one item for sale and receives successive offers drawn from some value distributions. The decision on whether or not to accept an offer is irrevocable, and the value distributions are only partially known. We therefore let the seller adopt a robust maximin strategy, assuming that value distributions are chosen adversarially by nature to minimize the value of the accepted offer. We provide a general maximin solution to this stopping problem that identifies the optimal (threshold-based) stopping rule for the seller for all statistical information structures. We then perform a detailed analysis for when the seller knows the common mean, dispersion (variance or mean absolute deviation) and support of the distributions. We show for this information structure that the seller's stopping rule consists of decreasing thresholds converging to the common mean, and that nature's adversarial response, in the long run, is to always create an all-or-nothing scenario. The maximin solutions also reveal what happens as dispersion or the number of offers grows large.