A structure-preserving variational discretization scheme for the Cahn-Hilliard Navier-Stokes system

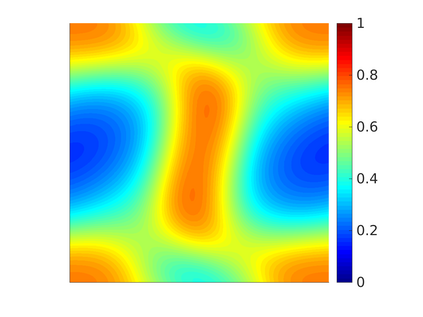
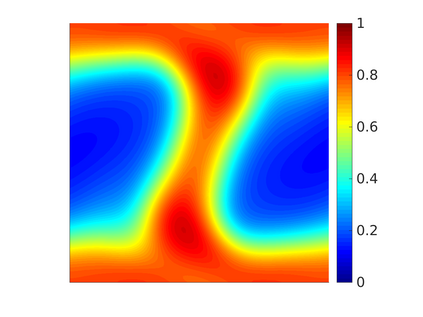
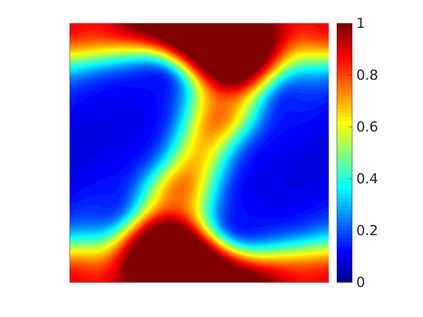
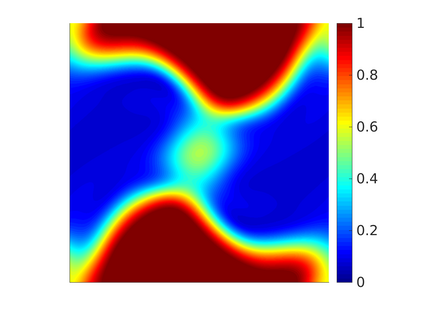
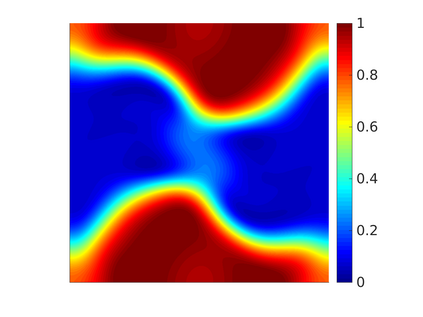
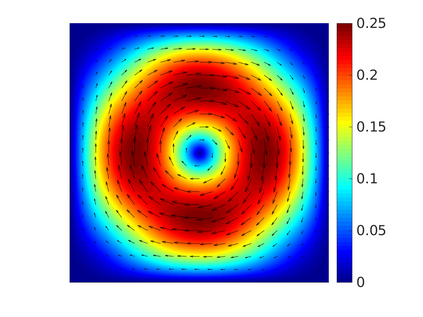
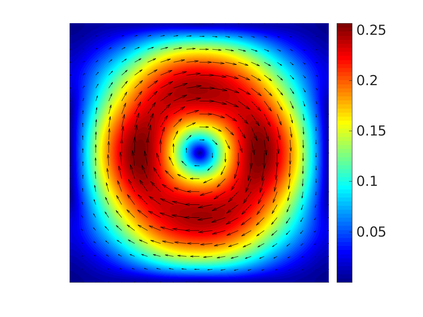
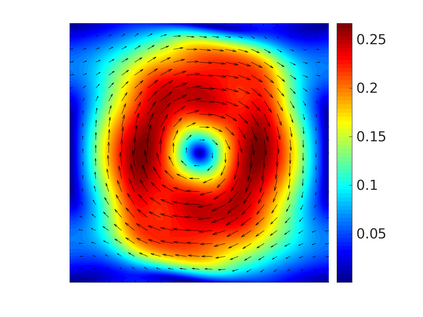
We propose and analyze a novel structure-preserving space-time variational discretization method for the Cahn-Hilliard-Navier-Stokes system with concentration dependent mobility and viscosity. Uniqueness and stability for the discrete problem is established in the presence of nonlinear model parameters by means of the relative energy estimates. Order optimal convergence rates with respect to space and time are proven for all variables using balanced approximation spaces and relaxed regularity conditions on the solution. Numerical tests are presented to demonstrate the reliability of the proposed scheme and to illustrate the theoretical findings.