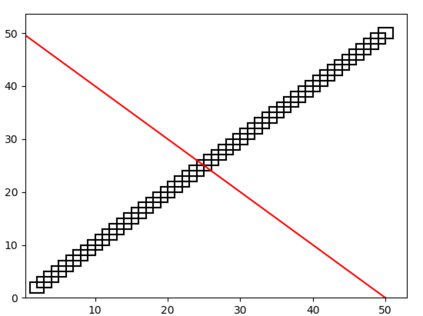
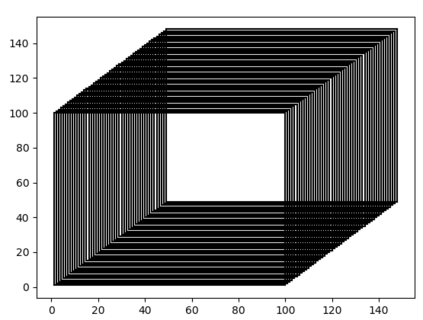
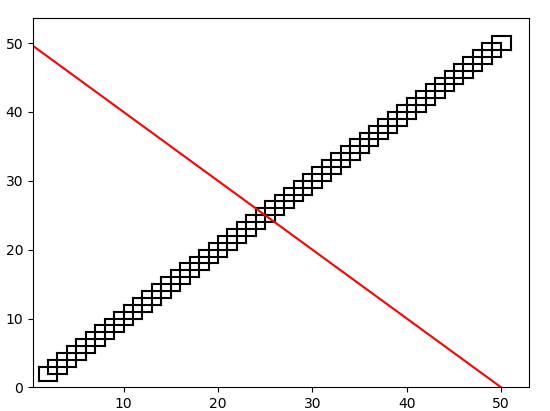
We study the problem of learning a finite union of integer (axis-aligned) hypercubes over the d-dimensional integer lattice, i.e., whose edges are parallel to the coordinate axes. This is a natural generalization of the classic problem in the computational learning theory of learning rectangles. We provide a learning algorithm with access to a minimally adequate teacher (i.e. membership and equivalence oracles) that solves this problem in polynomial-time, for any fixed dimension d. Over a non-fixed dimension, the problem subsumes the problem of learning DNF boolean formulas, a central open problem in the field. We have also provided extensions to handle infinite hypercubes in the union, as well as showing how subset queries could improve the performance of the learning algorithm in practice. Our problem has a natural application to the problem of monadic decomposition of quantifier-free integer linear arithmetic formulas, which has been actively studied in recent years. In particular, a finite union of integer hypercubes correspond to a finite disjunction of monadic predicates over integer linear arithmetic (without modulo constraints). Our experiments suggest that our learning algorithms substantially outperform the existing algorithms.
翻译:我们研究的是,在 d- 维整整形( 轴对齐) 超立方体的有限结合上, 即, 其边缘与坐标轴平行。 这是在学习矩形的计算学习理论中典型问题的自然概括性。 我们提供一种学习算法, 使用最起码的足够教师( 即会籍和等效或触须) 来解决在任何固定的维度中 的多元- 自由线性计算公式问题。 在非固定的维度中, 问题包含学习 DNF 布伦公式的问题, 这是这个领域的一个中心开放问题。 我们还提供了处理联盟中无限超立方体的扩展, 并展示了子查询如何改善学习算法的实际表现。 我们的问题自然地适用于近些年来一直积极研究过的多元化无定调的线性线性计算公式问题。 特别是, 直线性超立方体组合的有限结合了一个有限的调调调调, 与我们当前定型算法的定数性演算法的不比。