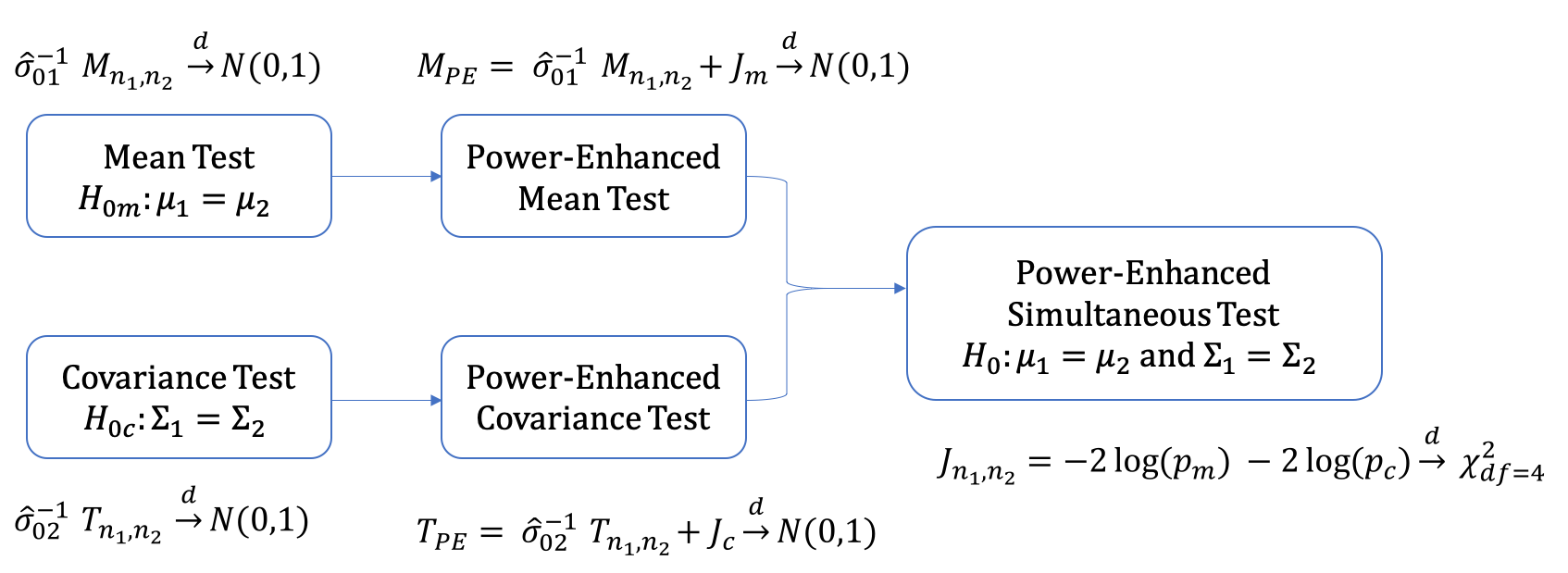
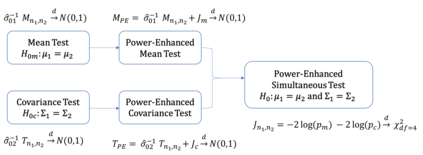
Power-enhanced tests with high-dimensional data have received growing attention in theoretical and applied statistics in recent years. Existing tests possess their respective high-power regions, and we may lack prior knowledge about the alternatives when testing for a problem of interest in practice. There is a critical need of developing powerful testing procedures against more general alternatives. This paper studies the joint test of two-sample mean vectors and covariance matrices for high-dimensional data. We first expand the high-power region of high-dimensional mean tests or covariance tests to a wider alternative space and then combine their strengths together in the simultaneous test. We develop a new power-enhanced simultaneous test that is powerful to detect differences in either mean vectors or covariance matrices under either sparse or dense alternatives. We prove that the proposed testing procedures align with the power enhancement principles introduced by Fan et al. (2015) and achieve the accurate asymptotic size and consistent asymptotic power. We demonstrate the finite-sample performance using simulation studies and a real application to find differentially expressed gene-sets in cancer studies. Our findings in the empirical study are supported by the biological literature.
翻译:近些年来,高维数据的强力强化测试在理论和应用统计中日益受到重视。现有测试拥有各自的高能区域,在实践上测试某个问题时,我们可能缺乏关于替代品的先行知识。非常需要针对更普遍的替代品制定强有力的测试程序。本文研究高维数据双层平均矢量和共变矩阵的联合测试。我们首先将高度中位测试或共变测试的高能区域扩大到更广泛的替代空间,然后在同时测试中将其优势结合起来。我们开发了一种新的增强力同时测试,在稀薄或密集的替代品下,能够发现中值矢量或共变异矩阵的差异。我们证明拟议的测试程序符合范等人提出的增强能力原则(2015年),并实现准确的零星尺寸和惯性能量。我们通过模拟研究和实际应用来发现癌症研究中的有差异的基因定位。我们的经验研究中的调查结果得到了生物文献的支持。