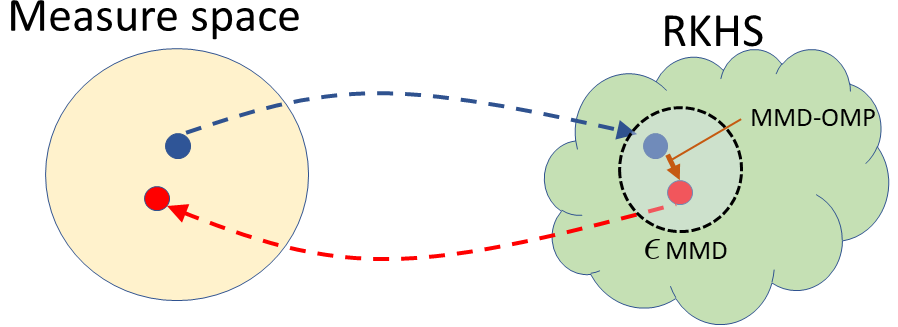
In Bayesian inference, we seek to compute information about random variables such as moments or quantiles on the basis of {available data} and prior information. When the distribution of random variables is {intractable}, Monte Carlo (MC) sampling is usually required. {Importance sampling is a standard MC tool that approximates this unavailable distribution with a set of weighted samples.} This procedure is asymptotically consistent as the number of MC samples (particles) go to infinity. However, retaining infinitely many particles is intractable. Thus, we propose a way to only keep a \emph{finite representative subset} of particles and their augmented importance weights that is \emph{nearly consistent}. To do so in {an online manner}, we (1) embed the posterior density estimate in a reproducing kernel Hilbert space (RKHS) through its kernel mean embedding; and (2) sequentially project this RKHS element onto a lower-dimensional subspace in RKHS using the maximum mean discrepancy, an integral probability metric. Theoretically, we establish that this scheme results in a bias determined by a compression parameter, which yields a tunable tradeoff between consistency and memory. In experiments, we observe the compressed estimates achieve comparable performance to the dense ones with substantial reductions in representational complexity.
翻译:在Bayesian 推论中, 我们试图根据 { 现有数据} 和先前的信息来计算随机变量的信息, 如时间或数量等随机变量的信息。 当随机变量的分布是{ 可吸引} 时, 通常需要 Monte Carlo (MC) 取样。 { 进口抽样是标准的MC 工具, 与一组加权样本相近于这种无法提供的分布 。} 这个程序在时间上是完全一致的, 因为 MC 样本的数量( 粒子) 将嵌入无限。 但是, 保留无限多颗粒是难以解决的。 因此, 我们建议一种方法, 仅保留一个\ emph{ 绝对代表粒子及其增加的重要性重量的 {emph{ 几乎一致 } 。 要这样做 { { 以 在线方式 } 。 { { 采样是一个标准的 MC 标准 MC 工具, 将远端点的密度估计 嵌入一个再生内核的 Hilbert 空间 。 } ; 和 (2) 连续地 将这个 RKHHS 元素 元素设到一个低维次空间的子空间 。