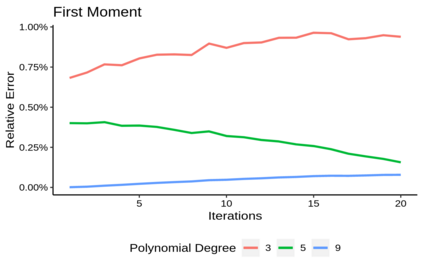
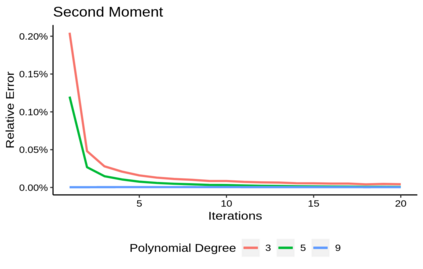
We present a method to automatically approximate moment-based invariants of probabilistic programs with non-polynomial updates of continuous state variables to accommodate more complex dynamics. Our approach leverages polynomial chaos expansion to approximate non-linear functional updates as sums of orthogonal polynomials. We exploit this result to automatically estimate state-variable moments of all orders in Prob-solvable loops with non-polynomial updates. We showcase the accuracy of our estimation approach in several examples, such as the turning vehicle model and the Taylor rule in monetary policy.
翻译:我们提出一种方法,以非球状状态变量和非球状更新来自动估计概率方案的时位变异性,以适应更复杂的动态。我们的方法是利用多球混乱扩张来将非线状功能更新作为正弦多球体的总和。我们利用这一结果,以非球状的更新来自动估计Prob-可溶性循环中所有订单的状态可变时数。我们在若干例子中展示了我们估算方法的准确性,例如转换车辆模型和泰勒在货币政策中的规则。