On the Universality of Langevin Diffusion for Private Euclidean (Convex) Optimization

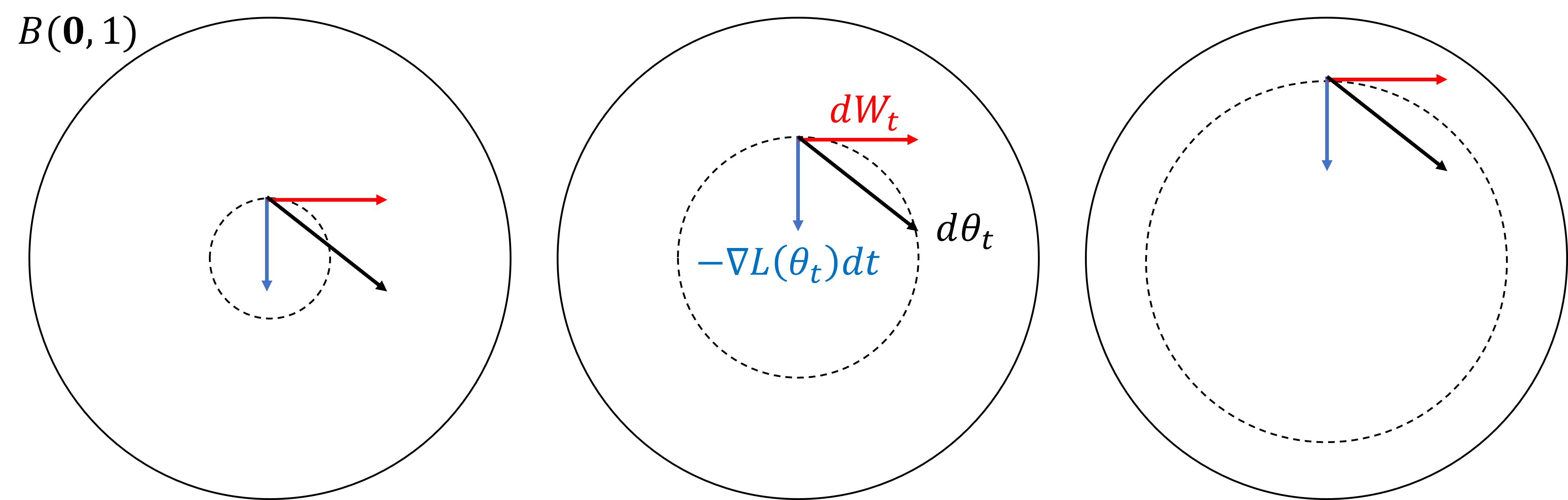
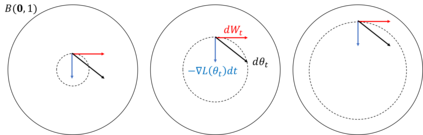
In this paper we revisit the problem of differentially private empirical risk minimization (DP-ERM) and differentially private stochastic convex optimization (DP-SCO). We show that a well-studied continuous time algorithm from statistical physics, called Langevin diffusion (LD), simultaneously provides optimal privacy/utility trade-offs for both DP-ERM and DP-SCO, under $\epsilon$-DP, and $(\epsilon,\delta)$-DP both for convex and strongly convex loss functions. We provide new time and dimension independent uniform stability properties of LD, using with we provide the corresponding optimal excess population risk guarantees for $\epsilon$-DP. An important attribute of our DP-SCO guarantees for $\epsilon$-DP is that they match the non-private optimal bounds as $\epsilon\to\infty$. Along the way, we provide various technical tools, which can be of independent interest: i) A new R\'enyi divergence bound for LD, when run on loss functions over two neighboring data sets, ii) Excess empirical risk bounds for last-iterate LD, analogous to that of Shamir and Zhang for noisy stochastic gradient descent (SGD), and iii) A two phase excess risk analysis of LD, where the first phase is when the diffusion has not converged in any reasonable sense to a stationary distribution, and in the second phase when the diffusion has converged to a variant of Gibbs distribution. Our universality results crucially rely on the dynamics of LD. When it has converged to a stationary distribution, we obtain the optimal bounds under $\epsilon$-DP. When it is run only for a very short time $\propto 1/p$, we obtain the optimal bounds under $(\epsilon,\delta)$-DP. Here, $p$ is the dimensionality of the model space.