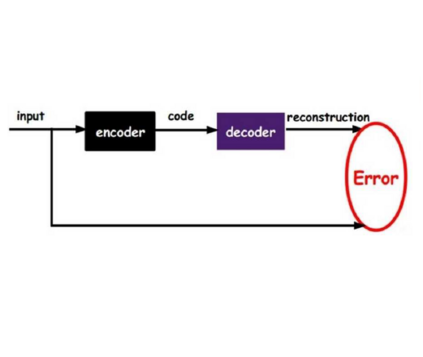
The outstanding performance of deep learning in various fields has been a fundamental query, which can be potentially examined using information theory that interprets the learning process as the transmission and compression of information. Information plane analyses of the mutual information between the input-hidden-output layers demonstrated two distinct learning phases of fitting and compression. It is debatable if the compression phase is necessary to generalize the input-output relations extracted from training data. In this study, we investigated this through experiments with various species of autoencoders and evaluated their information processing phase with an accurate kernel-based estimator of mutual information. Given sufficient training data, vanilla autoencoders demonstrated the compression phase, which was amplified after imposing sparsity regularization for hidden activities. However, we found that the compression phase is not universally observed in different species of autoencoders, including variational autoencoders, that have special constraints on network weights or manifold of hidden space. These types of autoencoders exhibited perfect generalization ability for test data without requiring the compression phase. Thus, we conclude that the compression phase is not necessary for generalization in representation learning.
翻译:不同领域深层学习的杰出表现是一个根本性的问题,可以使用将学习过程解释为信息传输和压缩的信息理论来研究。信息平流层对投入隐藏输出层之间相互信息的分析显示了两个不同的适应和压缩学习阶段。如果压缩阶段对于推广从培训数据中提取的输入-输出关系是必要的的话,这是值得商榷的。在本研究中,我们通过与各类自动计算器的实验来调查这一问题,并用精确的内核测算器来评估其信息处理阶段。考虑到足够的培训数据,香草胶自动计算器展示了压缩阶段,而压缩阶段在对隐蔽活动强制实行松散规范后得到了扩大。然而,我们发现,压缩阶段并不是在不同的自动计算器种类中普遍观察到的,包括变异自动算器,这些类型的自动计算器对网络重量或隐蔽空间的多重有特殊限制。这些类型的自动计算器在不要求压缩阶段的情况下对测试数据表现出完美的概括能力。因此,我们的结论是压缩阶段对于代表性学习一般来说并非必要。