Verified Neural Compressed Sensing

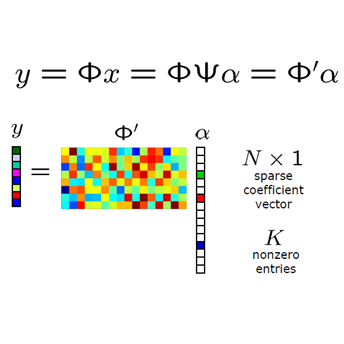
We develop the first (to the best of our knowledge) provably correct neural networks for a precise computational task, with the proof of correctness generated by an automated verification algorithm without any human input. Prior work on neural network verification has focused on partial specifications that, even when satisfied, are not sufficient to ensure that a neural network never makes errors. We focus on applying neural network verification to computational tasks with a precise notion of correctness, where a verifiably correct neural network provably solves the task at hand with no caveats. In particular, we develop an approach to train and verify the first provably correct neural networks for compressed sensing, i.e., recovering sparse vectors from a number of measurements smaller than the dimension of the vector. We show that for modest problem dimensions (up to 50), we can train neural networks that provably recover a sparse vector from linear and binarized linear measurements. Furthermore, we show that the complexity of the network (number of neurons/layers) can be adapted to the problem difficulty and solve problems where traditional compressed sensing methods are not known to provably work.