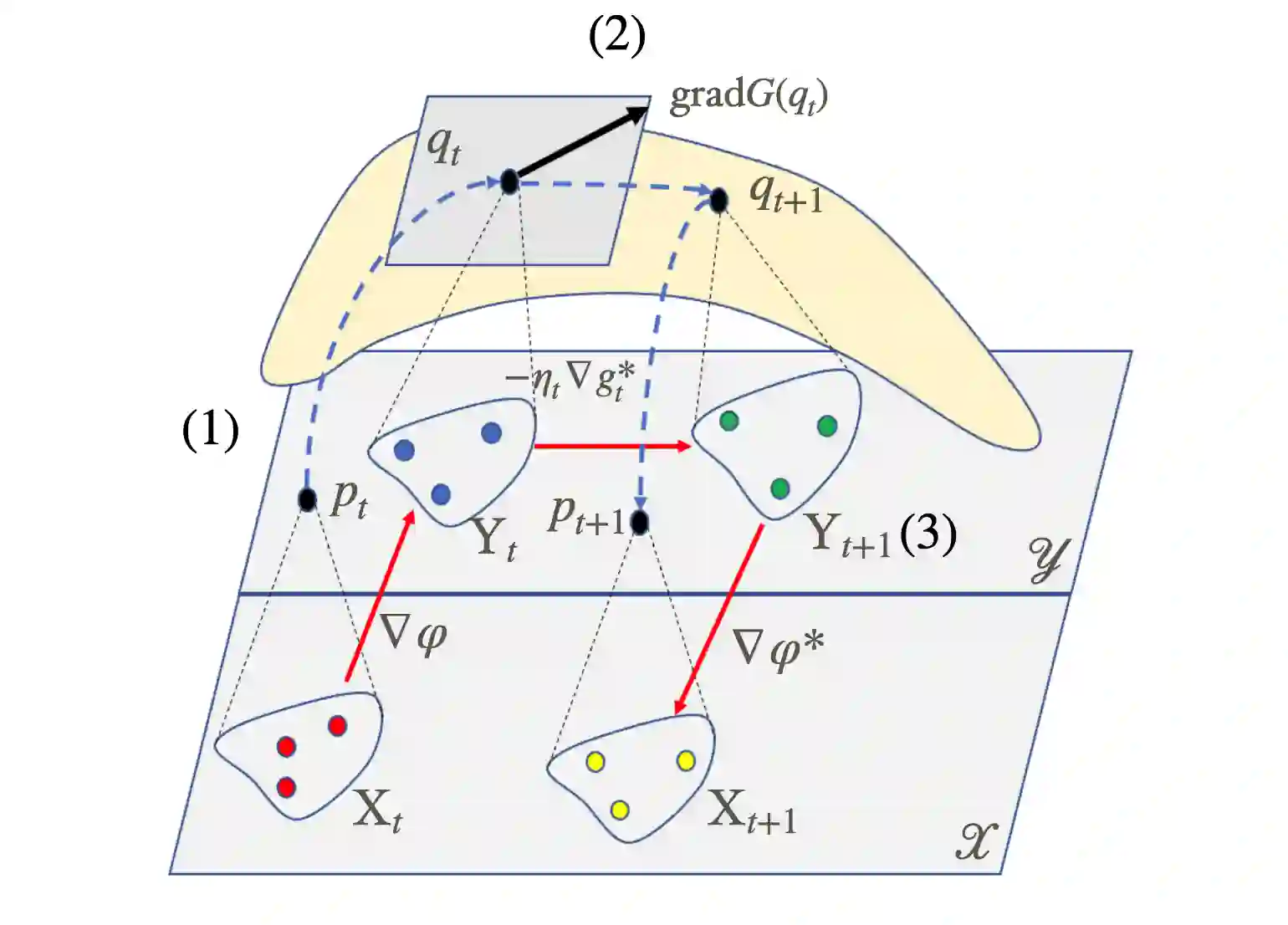
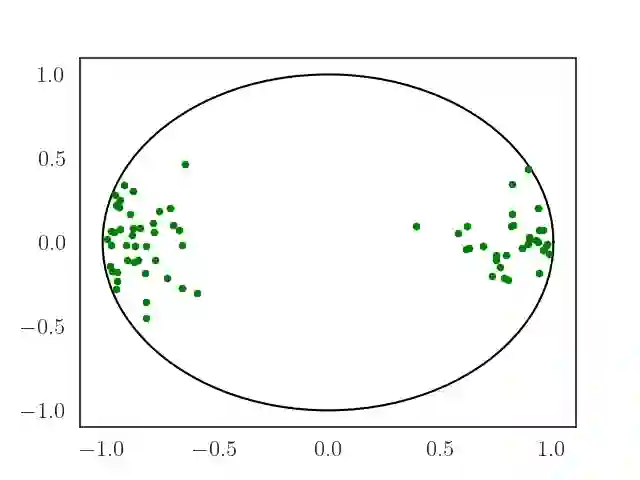
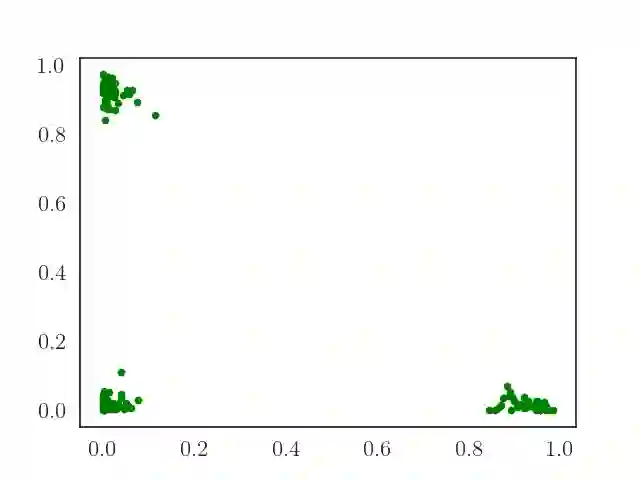
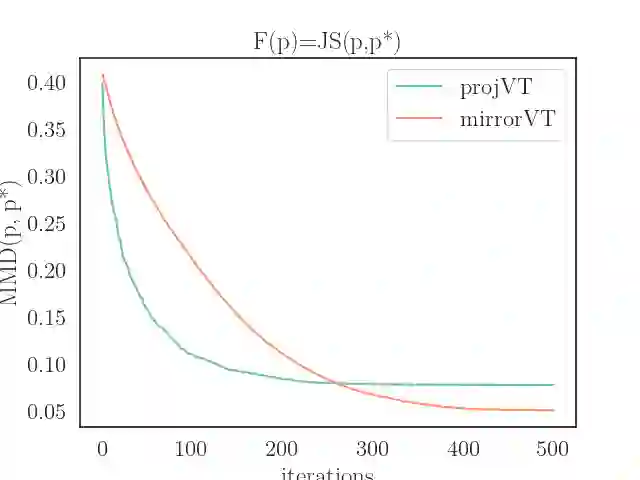
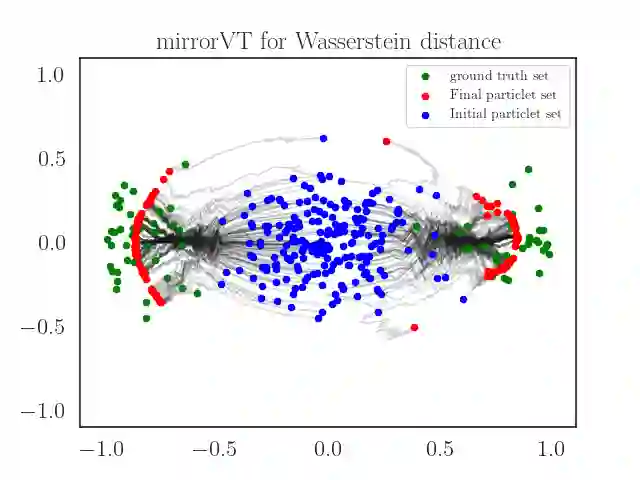
We consider the optimization problem of minimizing an objective functional, which admits a variational form and is defined over probability distributions on the constrained domain, which poses challenges to both theoretical analysis and algorithmic design. Inspired by the mirror descent algorithm for constrained optimization, we propose an iterative particle-based algorithm, named Mirrored Variational Transport (mirrorVT), extended from the Variational Transport framework [7] for dealing with the constrained domain. In particular, for each iteration, mirrorVT maps particles to an unconstrained dual domain induced by a mirror map and then approximately perform Wasserstein gradient descent on the manifold of distributions defined over the dual space by pushing particles. At the end of iteration, particles are mapped back to the original constrained domain. Through simulated experiments, we demonstrate the effectiveness of mirrorVT for minimizing the functionals over probability distributions on the simplex- and Euclidean ball-constrained domains. We also analyze its theoretical properties and characterize its convergence to the global minimum of the objective functional.
翻译:我们考虑了将目标功能最小化的优化问题,它允许一种变异形式,并且定义了限制域的概率分布,对理论分析和算法设计都提出了挑战。在限制优化的镜像下沉算法的启发下,我们提出了一个从变异运输框架[7] 延伸而来的基于粒子的迭代算法,名为镜像变异运输(mirrorVT),用于处理受限制域。特别是,对于每个迭代,镜像VT将粒子映射到由镜像地图引导的不受限制的双重域,然后通过推粒子在双空间定义的分布方块上大致地进行瓦瑟斯坦梯度下降。在迭代后,粒子被映射回到原来的受限制域。通过模拟实验,我们展示了镜像VT在将简单X和Euclidean球约束域的概率分布上的各种功能最小值。我们还分析了其理论属性,并描述其与目标功能全球最低值的趋同性。