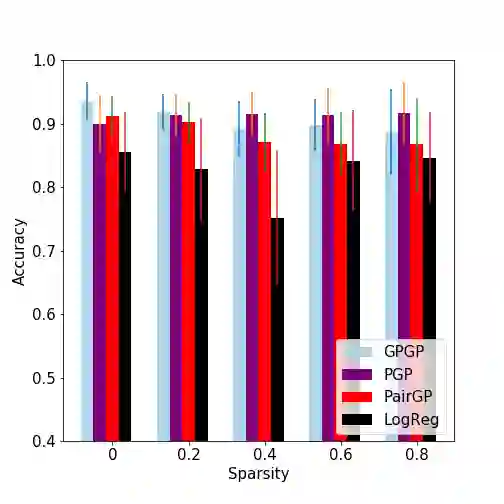
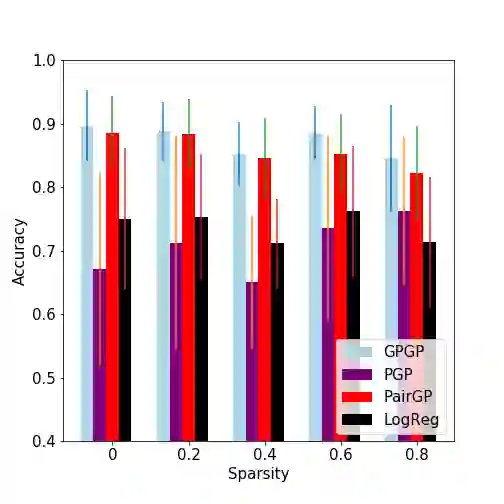
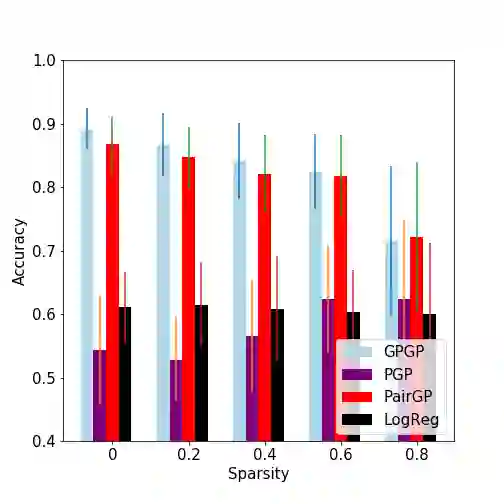
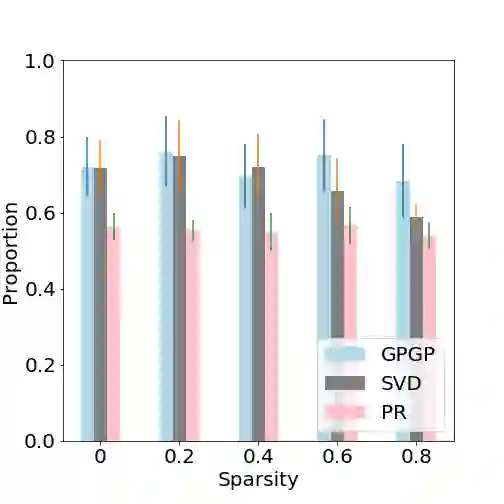
We revisit widely used preferential Gaussian processes by Chu et al.(2005) and challenge their modelling assumption that imposes rankability of data items via latent utility function values. We propose a generalisation of pgp which can capture more expressive latent preferential structures in the data and thus be used to model inconsistent preferences, i.e. where transitivity is violated, or to discover clusters of comparable items via spectral decomposition of the learned preference functions. We also consider the properties of associated covariance kernel functions and its reproducing kernel Hilbert Space (RKHS), giving a simple construction that satisfies universality in the space of preference functions. Finally, we provide an extensive set of numerical experiments on simulated and real-world datasets showcasing the competitiveness of our proposed method with state-of-the-art. Our experimental findings support the conjecture that violations of rankability are ubiquitous in real-world preferential data.
翻译:我们建议对数据中能够捕捉到更明显的潜在优惠结构,从而用来模拟不一致的偏好模式,即:在中转性受到侵犯的情况下,或者通过光谱分解学到的偏好功能来发现可比较的物品集群。 我们还考虑了相关共变内核功能的特性及其再生产内核Hilbert空间(RKHS)的特性,提供了满足偏好功能空间普遍性的简单构建。最后,我们对模拟和现实世界数据集提供了一套广泛的数字实验,展示了我们拟议方法与最新技术的竞争力。 我们的实验结论支持了这样的推测,即违反定级功能在现实世界的优惠数据中是普遍存在的。