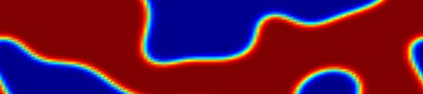
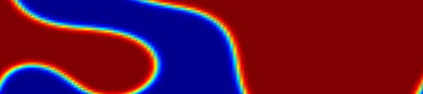
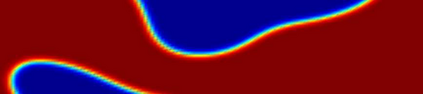
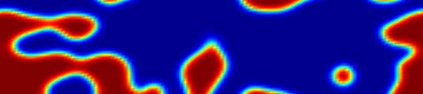
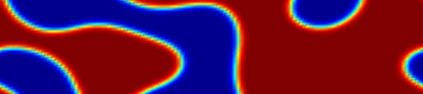
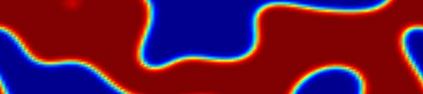
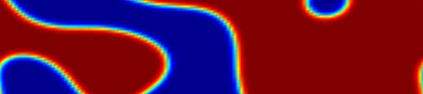
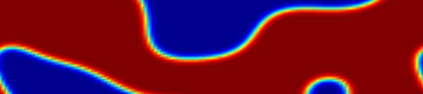
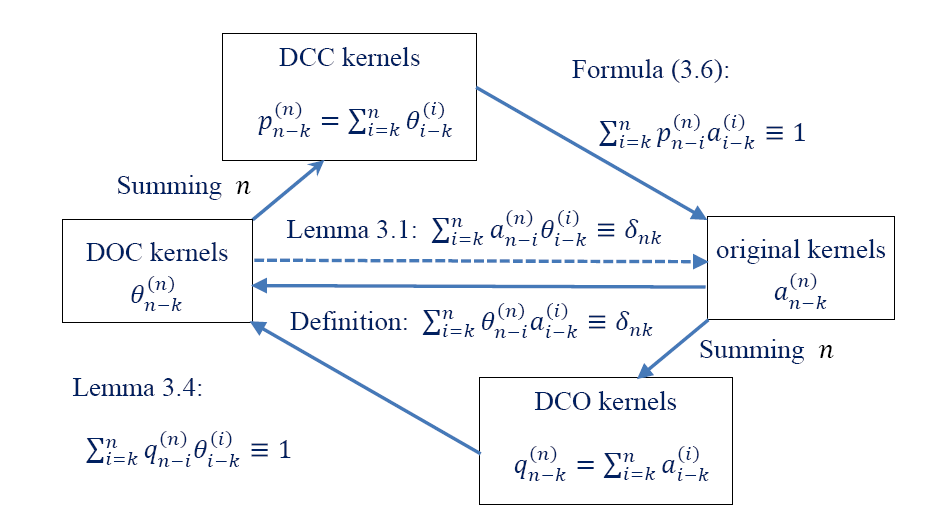
In this work, we propose a Crank-Nicolson-type scheme with variable steps for the time fractional Allen-Cahn equation. The proposed scheme is shown to be unconditionally stable (in a variational energy sense), and is maximum bound preserving. Interestingly, the discrete energy stability result obtained in this paper can recover the classical energy dissipation law when the fractional order $\alpha \rightarrow 1.$ That is, our scheme can asymptotically preserve the energy dissipation law in the $\alpha \rightarrow 1$ limit. This seems to be the first work on variable time-stepping scheme that can preserve both the energy stability and the maximum bound principle. Our Crank-Nicolson scheme is build upon a reformulated problem associated with the Riemann-Liouville derivative. As a by product, we build up a reversible transformation between the L1-type formula of the Riemann-Liouville derivative and a new L1-type formula of the Caputo derivative, with the help of a class of discrete orthogonal convolution kernels. This is the first time such a \textit{discrete} transformation is established between two discrete fractional derivatives. We finally present several numerical examples with an adaptive time-stepping strategy to show the effectiveness of the proposed scheme.
翻译:在这项工作中,我们提出了一个具有时间分数 Allen-Cahn 等式可变步骤的Crank- Nicolson 型计划。 拟议的计划显示无条件稳定( 变异能源意识 ), 并且具有最大约束性。 有趣的是, 本文获得的离散能源稳定性结果可以恢复经典能源消散法, 当分序 $\ alpha\ rightrow 1. 美元 时, 我们的计划可以在 $\ alpha\ rightrow $ rightrow $ 1 的分数制中, 自动保存能量消散法。 这似乎是关于可维护能源稳定性和最大约束原则的可变时间步制计划的首项工作。 我们的Crank- Nicolson 计划是在与Riemann- Liouville 衍生物相关的重订问题的基础上建立的。 作为产品, 我们建立了Riemann- Liouville 衍生物的L1- 型配方的L1型配方, 新的L1 型配方的配方制公式, 将帮助将一系列的离开的或深层次变正的公式 显示目前两个变型的变制的图式战略。 。