Fast estimation of a convolution type model for the intensity of spatial point processes

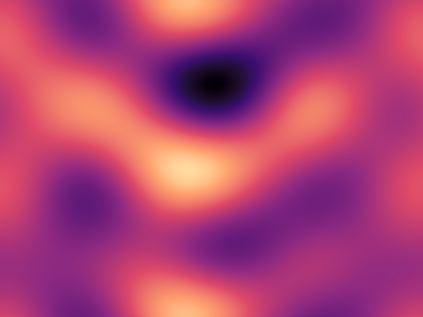
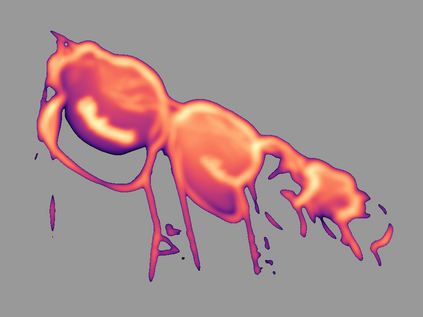
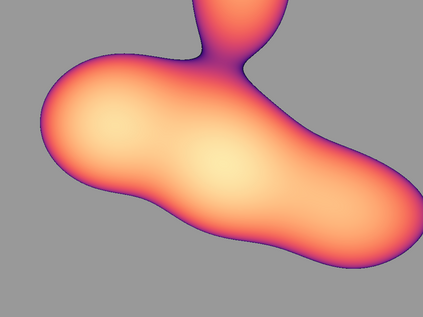
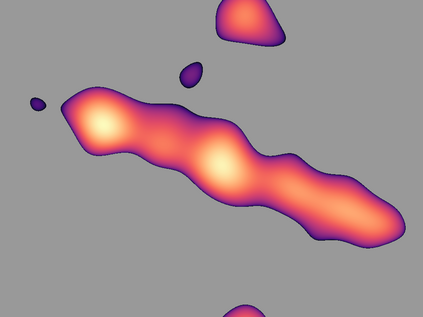
Estimating the first-order intensity function in point pattern analysis is an important problem, and it has been approached so far from different perspectives: parametrically, semiparametrically or nonparametrically. Our approach is close to a semiparametric one. Motivated by eye-movement data, we introduce a convolution type model where the log-intensity is modelled as the convolution of a function $\beta(\cdot)$, to be estimated, and a single spatial covariate (the image an individual is looking at for eye-movement data). Based on a Fourier series expansion, we show that the proposed model is related to the log-linear model with infinite number of coefficients, which correspond to the spectral decomposition of $\beta(\cdot)$. After truncation, we estimate these coefficients through a penalized Poisson likelihood and prove infill asymptotic results for a large class of spatial point processes. We illustrate the efficiency of the proposed methodology on simulated data and real data.