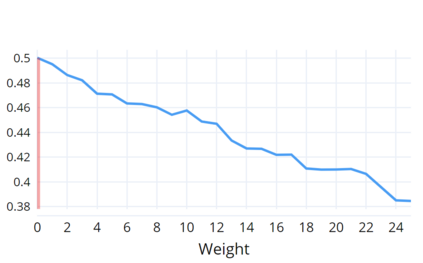
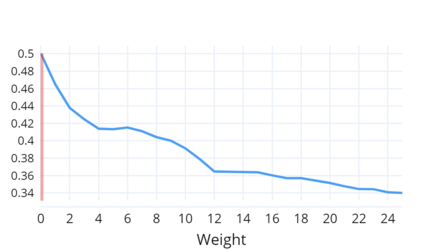
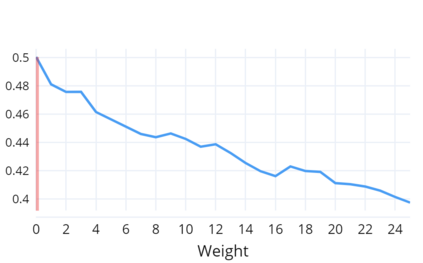
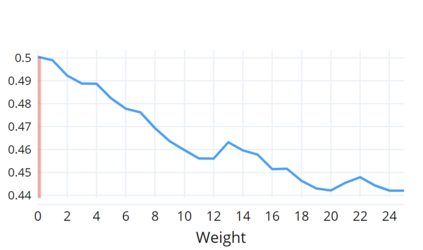
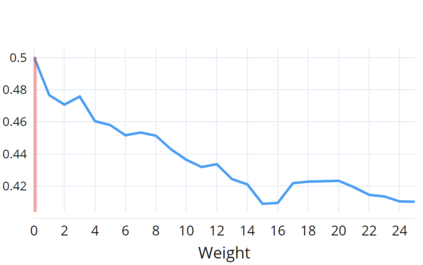
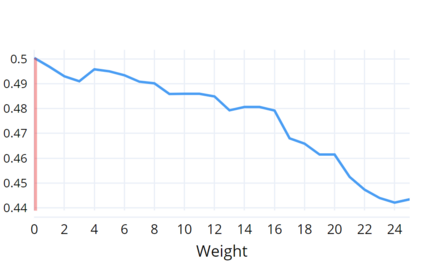
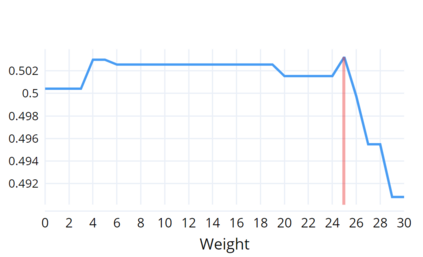
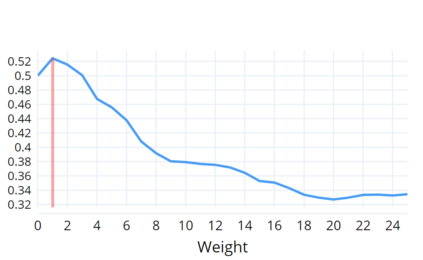
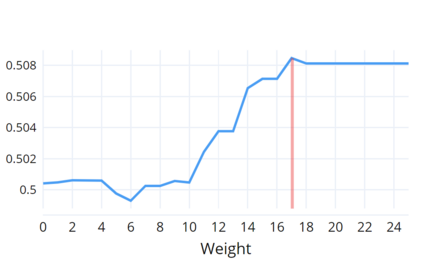
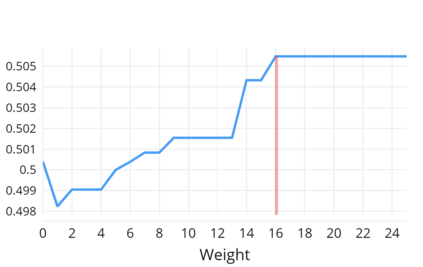
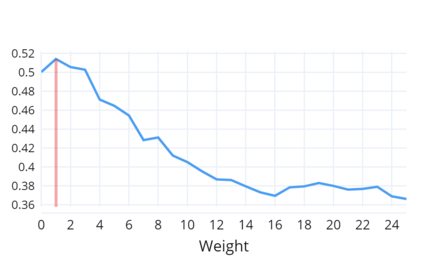
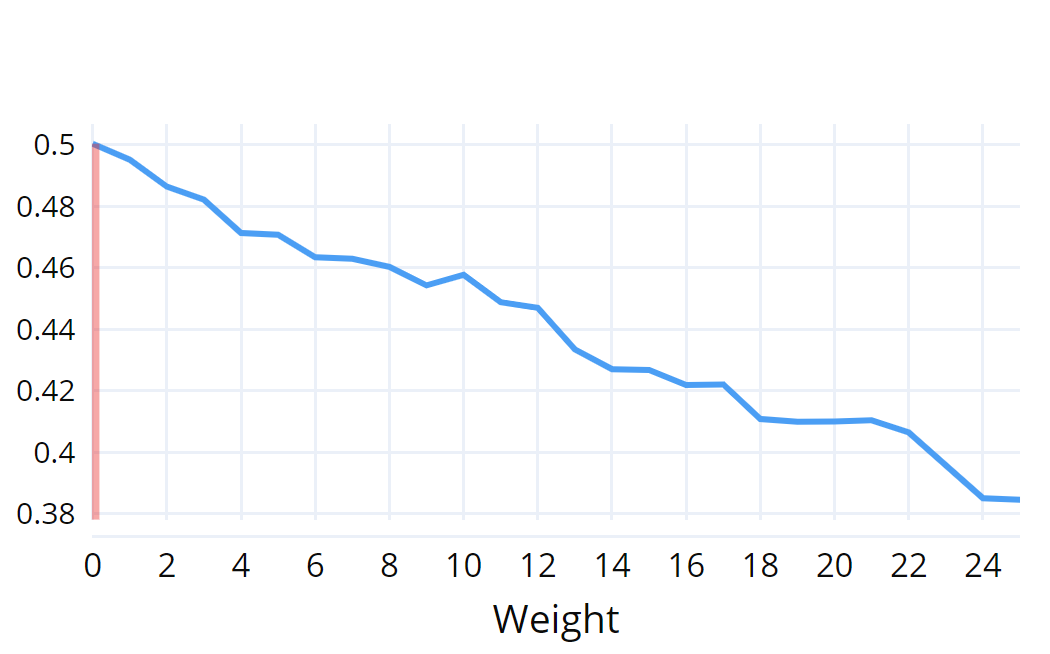
Indoor navigation systems leverage shortest path algorithms to calculate routes. In order to define the "shortest path", a cost function has to be specified based on theories and heuristics in the application domain. For the domain of indoor routing, we survey theories and criteria identified in the literature as essential for human path planning. We drive quantitative definitions and integrate them into a cost function that weights each of the criteria separately. We then apply an exhaustive grid search to find weights that lead to an ideal cost function. "Ideal" here is defined as guiding the algorithm to plan routes that are most similar to those chosen by humans. To explore which criteria should be taken into account in an improved pathfinding algorithm, eleven different factors whose favorable impact on route selection has been established in past research were considered. Each factor was included separately in the Dijkstra algorithm and the similarity of thus calculated routes to the actual routes chosen by students at the University of Regensburg was determined. This allows for a quantitative assessment of the factors' impact and further constitutes a way to directly compare them. A reduction of the number of turns, streets, revolving doors, entryways, elevators as well as the combination of the aforementioned factors was found to have a positive effect and generate paths that were favored over the shortest path. Turns and the combination of criteria turned out to be most impactful.
翻译:室内导航系统利用最短路径算法来计算路线。为了定义“最差路径”,必须根据应用领域的理论和超自然学确定成本功能。对于室内路线领域,我们调查文献中确认的对人类路径规划至关重要的理论和标准。我们驱动定量定义并将其纳入成本函数,分别加权每项标准。然后我们应用详尽的网格搜索,以找到导致理想成本功能的加权数。“理想”的定义是指导算法规划与人类选择的路线最相似的路线。为了探索在改进的路由算法中应考虑哪些标准。为了探索在改进的路由算法中确立对路线选择的有利影响,我们考虑了11个不同的因素,这些因素在以往的研究中已经确定了对路线选择的有利影响。每个因素都分别纳入了Dijkstra算法,从而确定了与Regensburg大学学生选择的实际路线的相似性。这样可以对各种因素的影响进行定量评估,并构成直接比较它们的方法。为了减少街道、旋转门、旋转门、进入通道的有利影响, 将最短通道和最接近的通道的组合结果归为上述的组合。