Design of false data injection attack on distributed process estimation

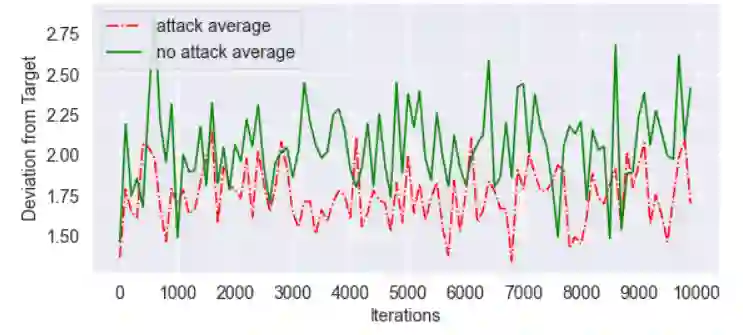
Herein, design of false data injection attack on a distributed cyber-physical system is considered. A stochastic process with linear dynamics and Gaussian noise is measured by multiple agent nodes, each equipped with multiple sensors. The agent nodes form a multi-hop network among themselves. Each agent node computes an estimate of the process by using its sensor observation and messages obtained from neighboring nodes, via Kalman-consensus filtering. An external attacker, capable of arbitrarily manipulating the sensor observations of some or all agent nodes, injects errors into those sensor observations. The goal of the attacker is to steer the estimates at the agent nodes as close as possible to a pre-specified value, while respecting a constraint on the attack detection probability. To this end, a constrained optimization problem is formulated to find the optimal parameter values of a certain class of linear attacks. The parameters of linear attack are learnt on-line via a combination of stochastic approximation based update of a Lagrange multiplier, and an optimization technique involving either the Karush-Kuhn-Tucker (KKT) conditions or online stochastic gradient descent. The problem turns out to be convex for some special cases. Desired convergence of the proposed algorithms are proved by exploiting the convexity and properties of stochastic approximation algorithms. Finally, numerical results demonstrate the efficacy of the attack.