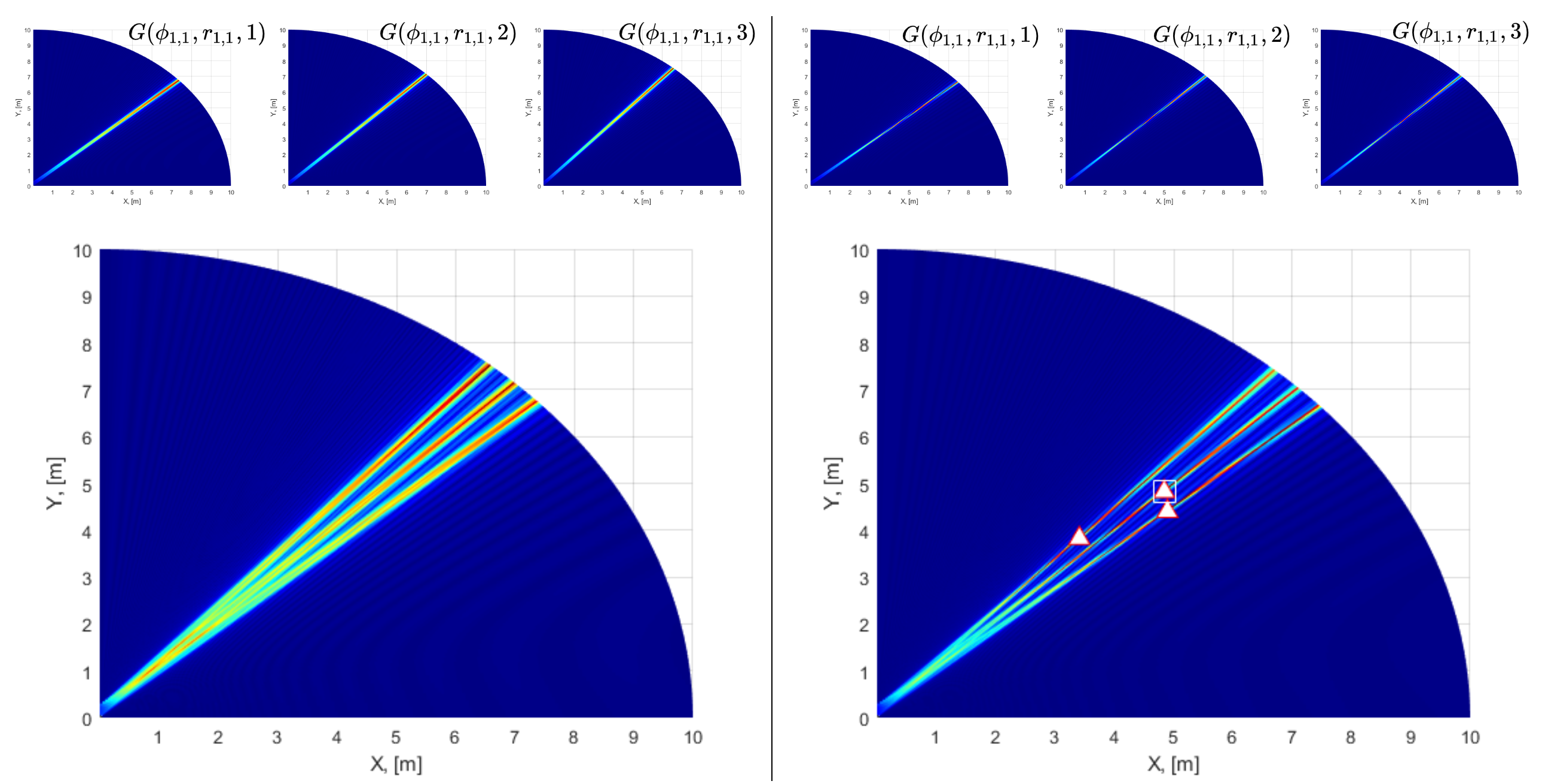
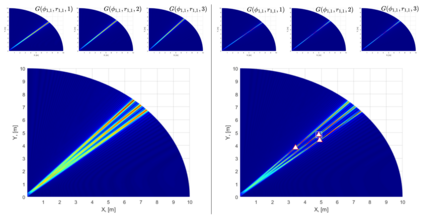
Terahertz (THz) band is expected to be one of the key enabling technologies of the sixth generation (6G) wireless networks because of its abundant available bandwidth and very narrow beam width. Due to high frequency operations, electrically small array apertures are employed, and the signal wavefront becomes spherical in the near-field. Therefore, near-field signal model should be considered for channel acquisition in THz systems. Unlike prior works which mostly ignore the impact of near-field beam-split (NB) and consider either narrowband scenario or far-field models, this paper introduces both a model-based and a model-free techniques for wideband THz channel estimation in the presence of NB. The model-based approach is based on orthogonal matching pursuit (OMP) algorithm, for which we design an NB-aware dictionary. The key idea is to exploit the angular and range deviations due to the NB. We then employ the OMP algorithm, which accounts for the deviations thereby ipso facto mitigating the effect of NB. We further introduce a federated learning (FL)-based approach as a model-free solution for channel estimation in a multi-user scenario to achieve reduced complexity and training overhead. Through numerical simulations, we demonstrate the effectiveness of the proposed channel estimation techniques for wideband THz systems in comparison with the existing state-of-the-art techniques.
翻译:Terahertz (Thz) 频段预计将成为第六代无线网络(6G) 的关键赋能技术之一, 因为它拥有丰富的带宽和非常狭窄的波束宽度。 由于高频操作, 使用了电小型阵列孔径, 信号波前沿在近场成为球形。 因此, 应考虑在Thz 系统中购买频道的近场信号模型。 与以前的工作不同, 以往的工作大多忽略了近场波段( Baam-split (NB) 的影响, 并考虑了窄带假想或远场模型, 本文既采用了基于模型的技术, 也采用了用于宽频带的Thaz频道估算的无模型技术。 基于模型的方法基于正方位匹配算算法(OMP), 我们为此设计了NB-aware字典的字典。 关键的想法是利用由于NB(NB) 而导致的角和范围偏差(NB) 的影响, 我们随后采用了OMP 算法, 从而从事实上减轻了NB的效应。 我们进一步引入了一种基于FL(FL) 宽的宽的广频频道评估方法,, 通过一个基于的广域模拟的模拟模拟系统, 以实现无数字化的模拟的模拟系统, 模拟的模拟的模拟系统, 的模拟的系统, 来显示为我们所拟议的高频路段模拟的模拟的模拟的系统, 的模拟的系统, 以实现无数字式的模拟的模拟的模拟的模拟的模拟的模拟的系统, 的模拟的模拟的模拟的模拟的系统, 的系统, 的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的系统, 的模拟的模拟的模拟的模拟的模拟, 的模拟的模拟的系统, 的模拟的模拟的模拟的模拟的系统, 的系统, 的模拟的系统, 的模拟的模拟的模拟, 的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的系统的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的系统的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的模拟的