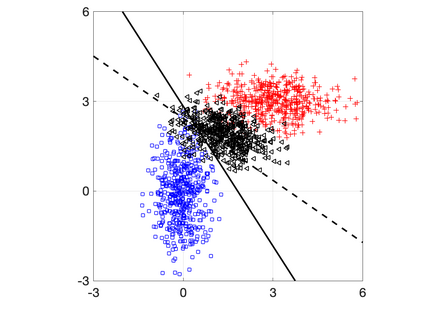
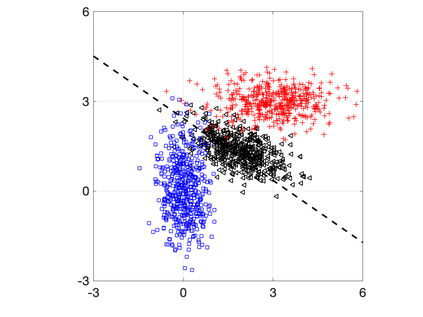
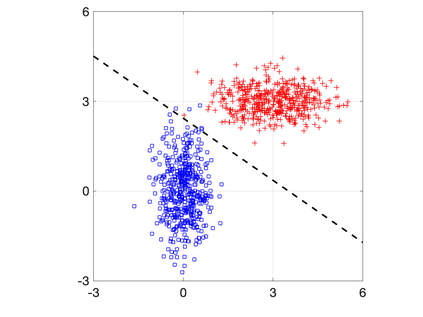
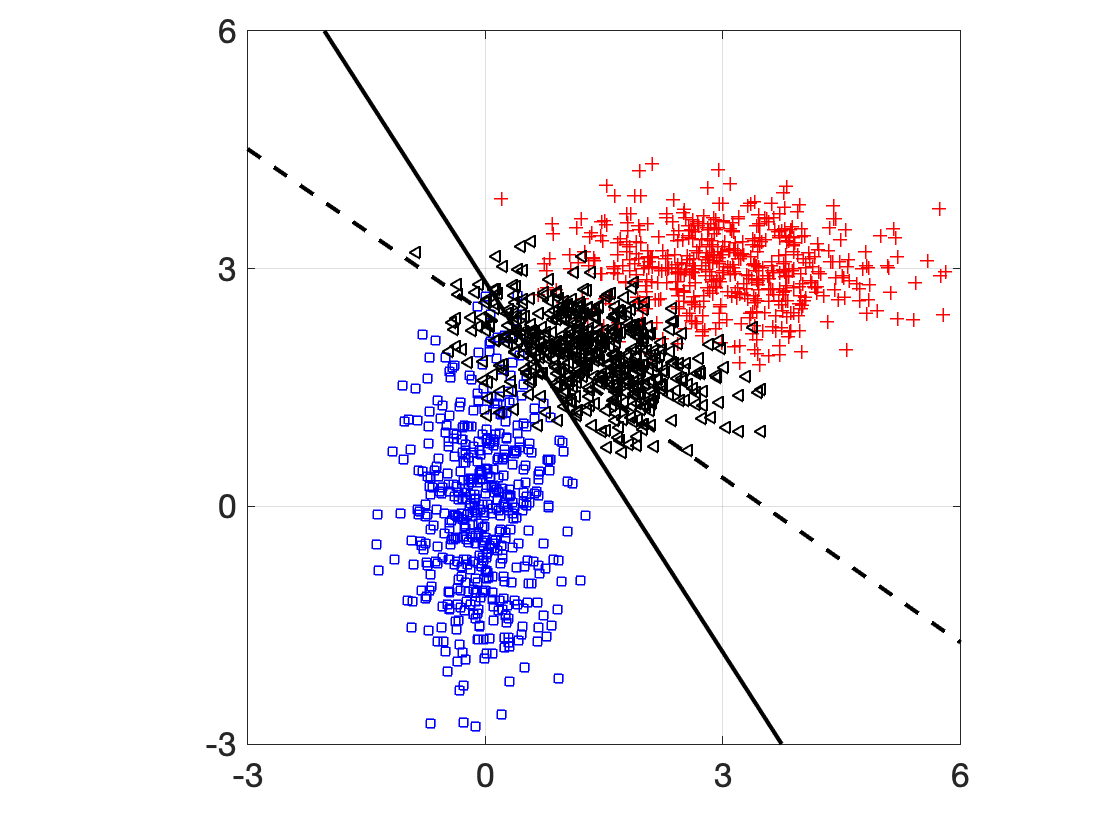
In this paper, we employ a game-theoretic model to analyze the interaction between an adversary and a classifier. There are two classes (i.e., positive and negative classes) to which data points can belong. The adversary is interested in maximizing the probability of miss-detection for the positive class (i.e., false negative probability). The adversary however does not want to significantly modify the data point so that it still maintains favourable traits of the original class. The classifier, on the other hand, is interested in maximizing the probability of correct detection for the positive class (i.e., true positive probability) subject to a lower-bound on the probability of correct detection for the negative class (i.e., true negative probability). For conditionally Gaussian data points (conditioned on the class) and linear support vector machine classifiers, we rewrite the optimization problems of the adversary and the classifier as convex optimization problems and use best response dynamics to learn an equilibrium of the game. This results in computing a linear support vector machine classifier that is robust against adversarial input manipulations. We illustrate the framework on a synthetic dataset and a public Cardiovascular Disease dataset.
翻译:在本文中, 我们使用一个游戏理论模型来分析对手和分类器之间的相互作用。 有两种类别( 即正和负类), 数据点可以归属于其中。 对手有意将正类( 假负概率) 的误检测概率最大化。 但是, 对手并不想显著修改数据点, 从而保持原始类的有利特性。 另一方面, 分类器有意为正类( 即真实正概率) 的正确检测概率最大化。 在对负类( 即真实概率) 进行正确检测的概率方面, 有两种类别( 正和负概率) 。 对手有意使正类( 即正负概率) 的概率最大化。 对于有条件的高斯数据点( 以类为条件) 和线性支持向量机分类器分类器分类, 我们重写对手和分类器的优化问题, 并使用最佳响应动态来学习游戏的平衡。 这导致计算线性支持向矢量分析器的分类器, 相对于对对抗性输入性输入操纵的磁盘。 我们演示了合成数据系统。