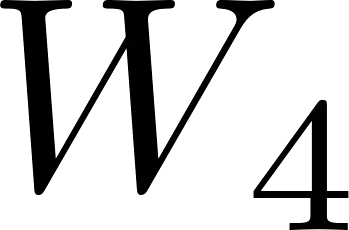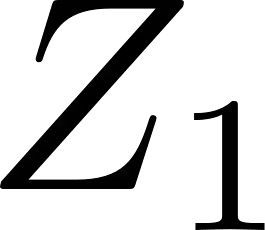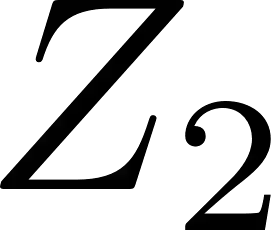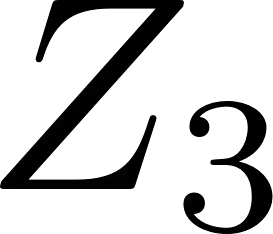In the robust secure aggregation problem, a server wishes to learn and only learn the sum of the inputs of a number of users while some users may drop out (i.e., may not respond). The identity of the dropped users is not known a priori and the server needs to securely recover the sum of the remaining surviving users. We consider the following minimal two-round model of secure aggregation. Over the first round, any set of no fewer than $U$ users out of $K$ users respond to the server and the server wants to learn the sum of the inputs of all responding users. The remaining users are viewed as dropped. Over the second round, any set of no fewer than $U$ users of the surviving users respond (i.e., dropouts are still possible over the second round) and from the information obtained from the surviving users over the two rounds, the server can decode the desired sum. The security constraint is that even if the server colludes with any $T$ users and the messages from the dropped users are received by the server (e.g., delayed packets), the server is not able to infer any additional information beyond the sum in the information theoretic sense. For this information theoretic secure aggregation problem, we characterize the optimal communication cost. When $U \leq T$, secure aggregation is not feasible, and when $U > T$, to securely compute one symbol of the sum, the minimum number of symbols sent from each user to the server is $1$ over the first round, and $1/(U-T)$ over the second round.
翻译:在强大的安全聚合问题中,服务器希望学习并且只学习一些用户的投入总和,而有些用户可能退出(即可能不回答)。在第二回合中,尚存用户的不少于美元的任何一组用户都会回答(即在第二回合中仍有可能收回),服务器需要从幸存用户获得的信息中安全收回剩余用户的总数。我们认为以下最低两轮安全集合模式:在第一轮中,任何不少于美元用户的一套不少于美元用户对服务器的反应($$),服务器希望了解所有响应用户的投入总和。其余用户被视为已下降。在第二轮中,幸存用户的任何一套不少于美元用户的用户的固定循环用户回答(即在第二回合中仍然有可能收回),从两回合中从幸存用户获得的信息中,服务器可以解码所希望的总额。在第一轮中,即使服务器与任何美元用户串联,而且用户发送的信息是可行的(例如,延迟的包装),服务器无法首先推断任何不少于美元的交易。