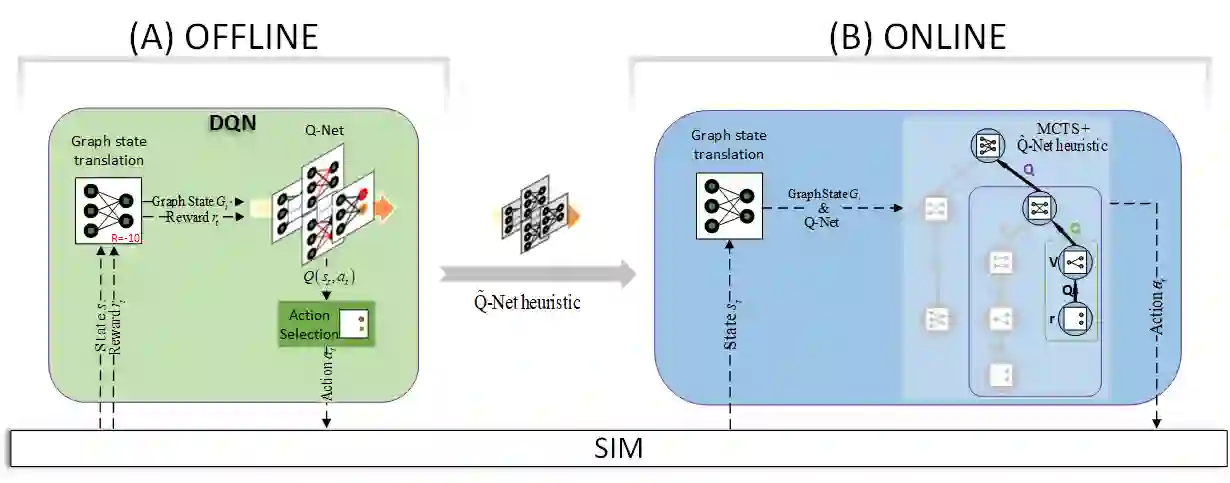
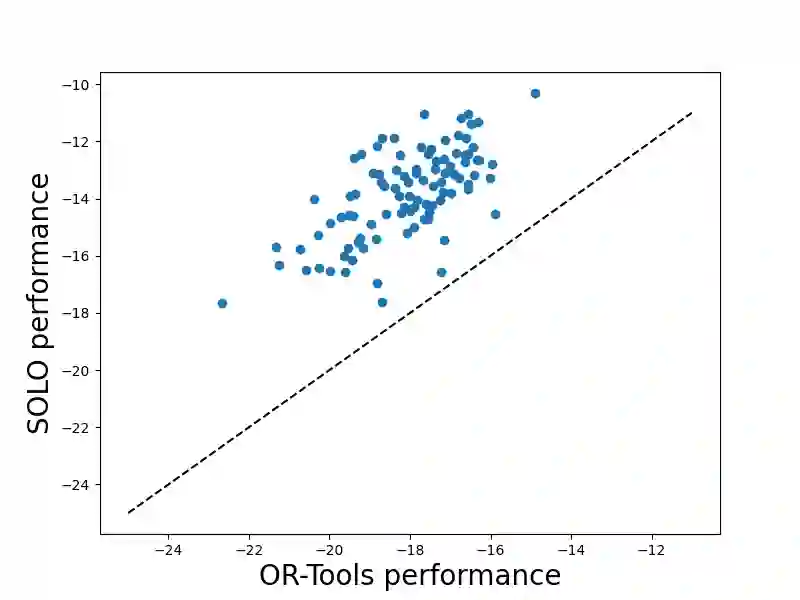
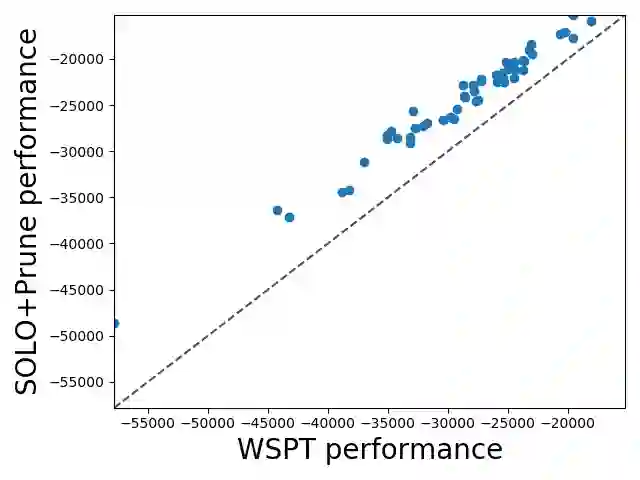
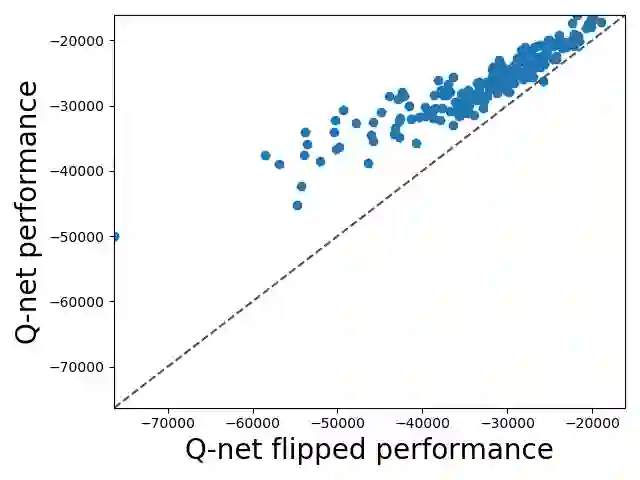
We study combinatorial problems with real world applications such as machine scheduling, routing, and assignment. We propose a method that combines Reinforcement Learning (RL) and planning. This method can equally be applied to both the offline, as well as online, variants of the combinatorial problem, in which the problem components (e.g., jobs in scheduling problems) are not known in advance, but rather arrive during the decision-making process. Our solution is quite generic, scalable, and leverages distributional knowledge of the problem parameters. We frame the solution process as an MDP, and take a Deep Q-Learning approach wherein states are represented as graphs, thereby allowing our trained policies to deal with arbitrary changes in a principled manner. Though learned policies work well in expectation, small deviations can have substantial negative effects in combinatorial settings. We mitigate these drawbacks by employing our graph-convolutional policies as non-optimal heuristics in a compatible search algorithm, Monte Carlo Tree Search, to significantly improve overall performance. We demonstrate our method on two problems: Machine Scheduling and Capacitated Vehicle Routing. We show that our method outperforms custom-tailored mathematical solvers, state of the art learning-based algorithms, and common heuristics, both in computation time and performance.
翻译:我们研究的是诸如机器排期、路由和任务等真实世界应用的组合问题。 我们提出一种将强化学习(RL)和规划相结合的方法。 这种方法同样可以适用于离线和在线的组合问题变式, 问题组成部分(如排期问题中的工作岗位)事先不为人知, 而在决策过程中抵达。 我们的解决方案非常通用、可扩展, 并且利用对问题参数的分布性知识。 我们将解决方案进程设计成一个 MDP, 并采取深Q学习方法, 将各州作为图表, 从而允许我们经过培训的政策以原则性的方式处理任意变化。 尽管所学的政策在期待中效果良好, 小偏差可能会对组合环境产生重大的负面影响。 我们通过在兼容的搜索算法( Monte Carlo Tree搜索)中以非最佳超能力超能力超能力来减轻这些偏差。 我们用两种问题来展示我们的方法: 机器排版和卡普里托拉·卡斯特拉· 亚德· 亚斯特洛· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·