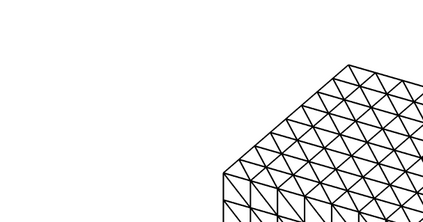
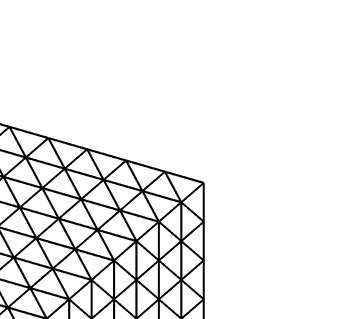
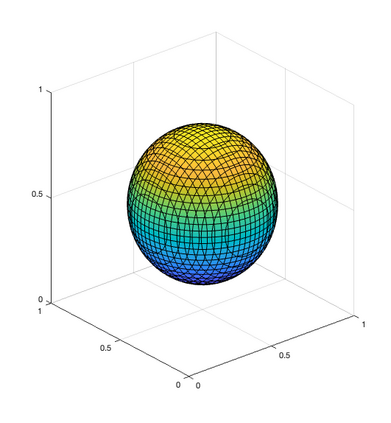
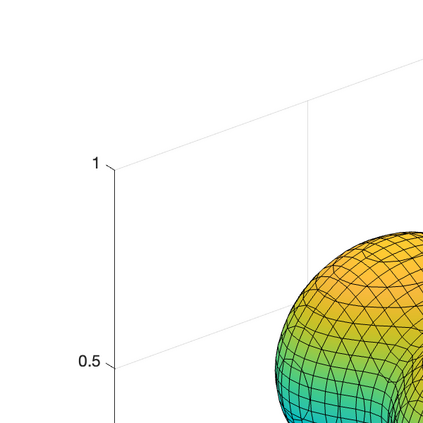
We propose and analyze an unfitted finite element method for solving elliptic problems on domains with curved boundaries and interfaces. The approximation space on the whole domain is obtained by the direct extension of the finite element space defined on interior elements, in the sense that there is no degree of freedom locating in boundary/interface elements. The boundary/jump conditions are imposed in a weak sense in the scheme. The method is shown to be stable without any mesh adjustment or any special stabilization. Optimal convergence rates under the $L^2$ norm and the energy norm are derived. Numerical results in both two and three dimensions are presented to illustrate the accuracy and the robustness of the method.
翻译:我们建议并分析一种不合适的有限要素方法,以解决具有曲线边界和界面的域的椭圆形问题;通过直接扩展内部各单元界定的有限要素空间,获得整个域的近似空间,因为边界/界面各单元没有一定程度的自由定位;边界/跳跃条件在计划内是以一种较弱的意义上强加的;该方法在没有任何网格调整或任何特别稳定的情况下都显示是稳定的;在2美元规范和能源规范下得出了最佳的趋同率;提出了两个和三个层面的数值结果,以说明方法的准确性和稳健性。
相关内容
- Today (iOS and OS X): widgets for the Today view of Notification Center
- Share (iOS and OS X): post content to web services or share content with others
- Actions (iOS and OS X): app extensions to view or manipulate inside another app
- Photo Editing (iOS): edit a photo or video in Apple's Photos app with extensions from a third-party apps
- Finder Sync (OS X): remote file storage in the Finder with support for Finder content annotation
- Storage Provider (iOS): an interface between files inside an app and other apps on a user's device
- Custom Keyboard (iOS): system-wide alternative keyboards
Source: iOS 8 Extensions: Apple’s Plan for a Powerful App Ecosystem