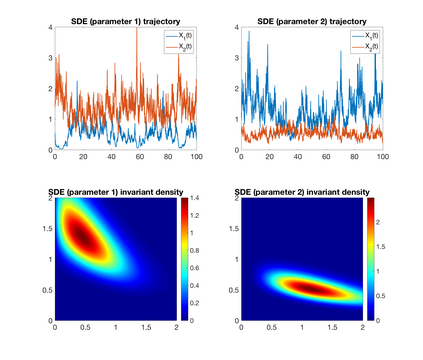
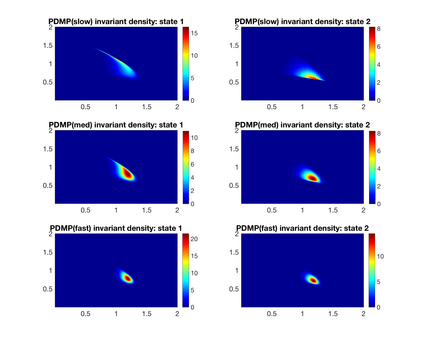
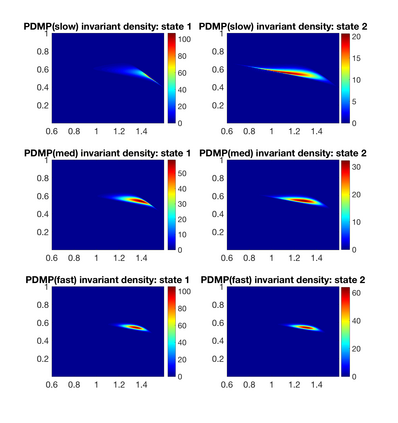
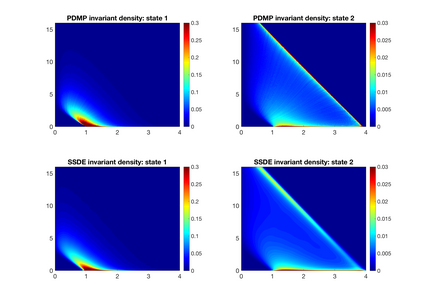
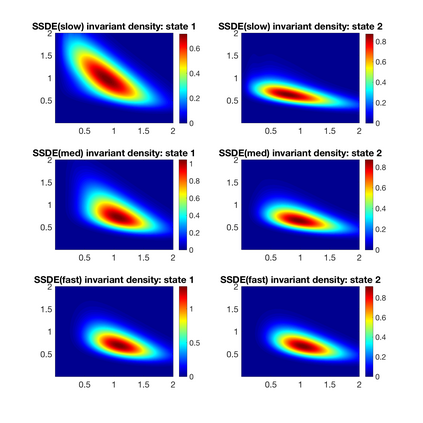
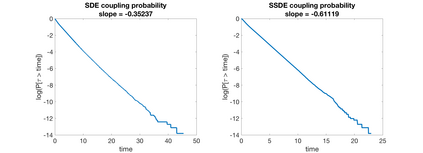
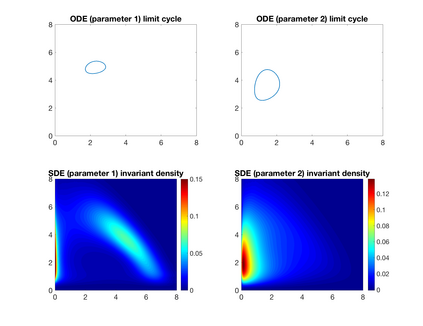
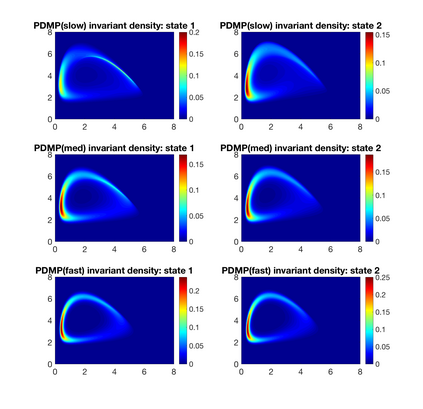
We analyze ecological systems that are influenced by random environmental fluctuations. We first provide general conditions which ensure that the species coexist and the system converges to a unique invariant probability measure (stationary distribution). Since it is usually impossible to characterize this invariant probability measure analytically, we develop a powerful method for numerically approximating invariant probability measures. This allows us to shed light upon how the various parameters of the ecosystem impact the stationary distribution. We analyze different types of environmental fluctuations. At first we study ecosystems modeled by stochastic differential equations. In the second setting we look at piecewise deterministic Markov processes. These are processes where one follows a system of differential equations for a random time, after which the environmental state changes, and one follows a different set of differential equations -- this procedure then gets repeated indefinitely. Finally, we look at stochastic differential equations with switching, which take into account both the white noise fluctuations and the random environmental switches. As applications of our theoretical and numerical analysis, we look at competitive Lotka--Volterra, Beddington-DeAngelis predator-prey, and rock-paper-scissors dynamics. We highlight new biological insights by analyzing the stationary distributions of the ecosystems and by seeing how various types of environmental fluctuations influence the long term fate of populations.
翻译:我们分析受随机环境波动影响的生态系统。 我们首先提供一般条件, 以确保物种共存, 并且系统会融合到一种独特的不定概率度量( 静态分布 ) 。 由于通常不可能用分析方法描述这种不定概率度量, 我们开发了一种强大的方法, 以数字相近的方式测量变化的概率度量。 这让我们可以揭示生态系统影响的各种参数是如何影响固定分布的。 我们分析不同类型的环境波动。 首先, 我们研究以随机差分方程式为模型的生态系统。 在第二个环境下, 我们审视了小巧的确定性马可夫过程。 这些过程中, 人们在随机的时间遵循一种差异方程式, 之后环境状态的变化, 并且遵循一套不同的差异方程式。 最后, 我们用开关来审视各种相近的相异方程式, 既考虑到白色噪音的波动, 也考虑到随机的环境开关。 作为我们理论和数字分析的应用, 我们从具有竞争力的洛特卡- Volterra, Beditton- Deangelis- Deangel 过程。 这些过程是随机的公式系统系统,, 之后环境状态变化变化, 和岩石分布变化的周期, 分析各种环境变化的动态, 和岩石分布的动态, 分析, 以及岩石分布的动态的动态的动态, 分析。