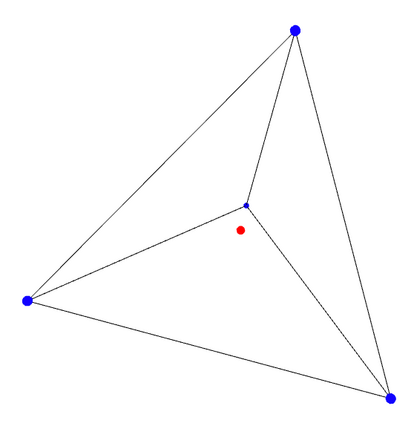
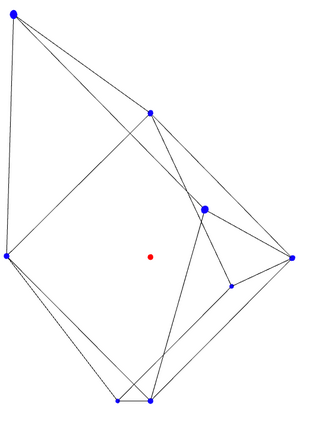
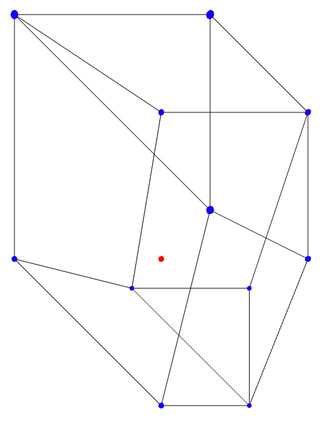
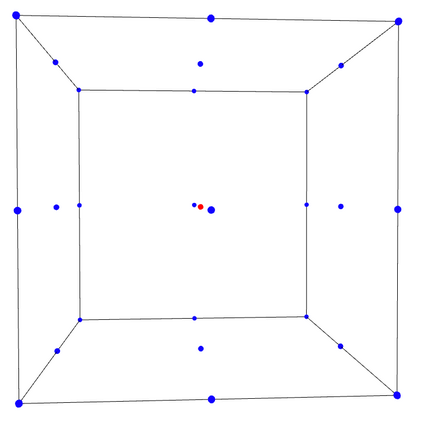
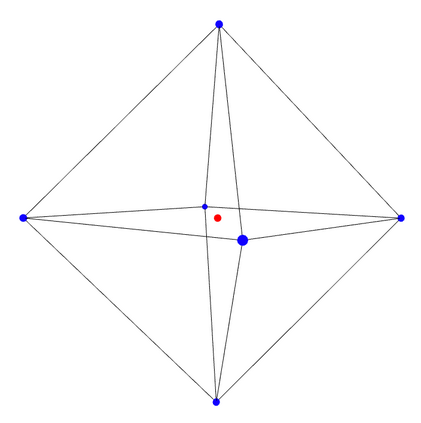
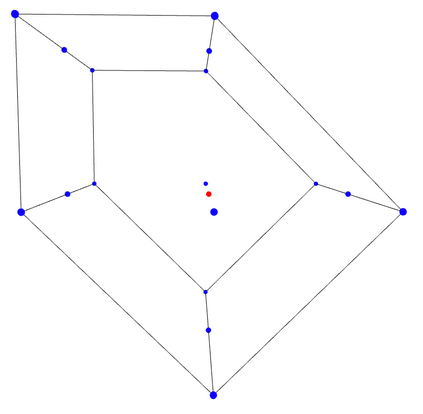
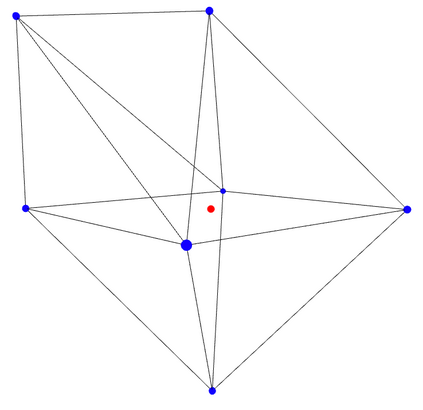
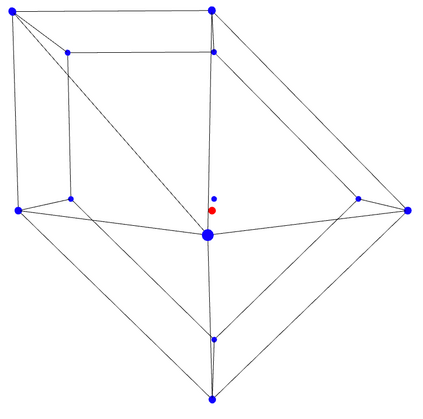
We study the problem of maximum likelihood (ML) estimation for statistical models defined by reflexive polytopes. Our focus is on the maximum likelihood degree of these models as an algebraic measure of complexity of the corresponding optimization problem. We compute the ML degrees of all 4319 classes of three-dimensional reflexive polytopes, and observe some surprising behavior in terms of the presence of gaps between ML degrees and degrees of the associated toric varieties. We interpret these drops in the context of discriminants and prove formulas for the ML degree for families of reflexive polytopes, including the hypercube and its dual, the cross polytope, in arbitrary dimension. In particular, we determine a family of embeddings for the $d$-cube that implies ML degree one. Finally, we discuss generalized constructions of families of reflexive polytopes in terms of their ML degrees.
翻译:暂无翻译