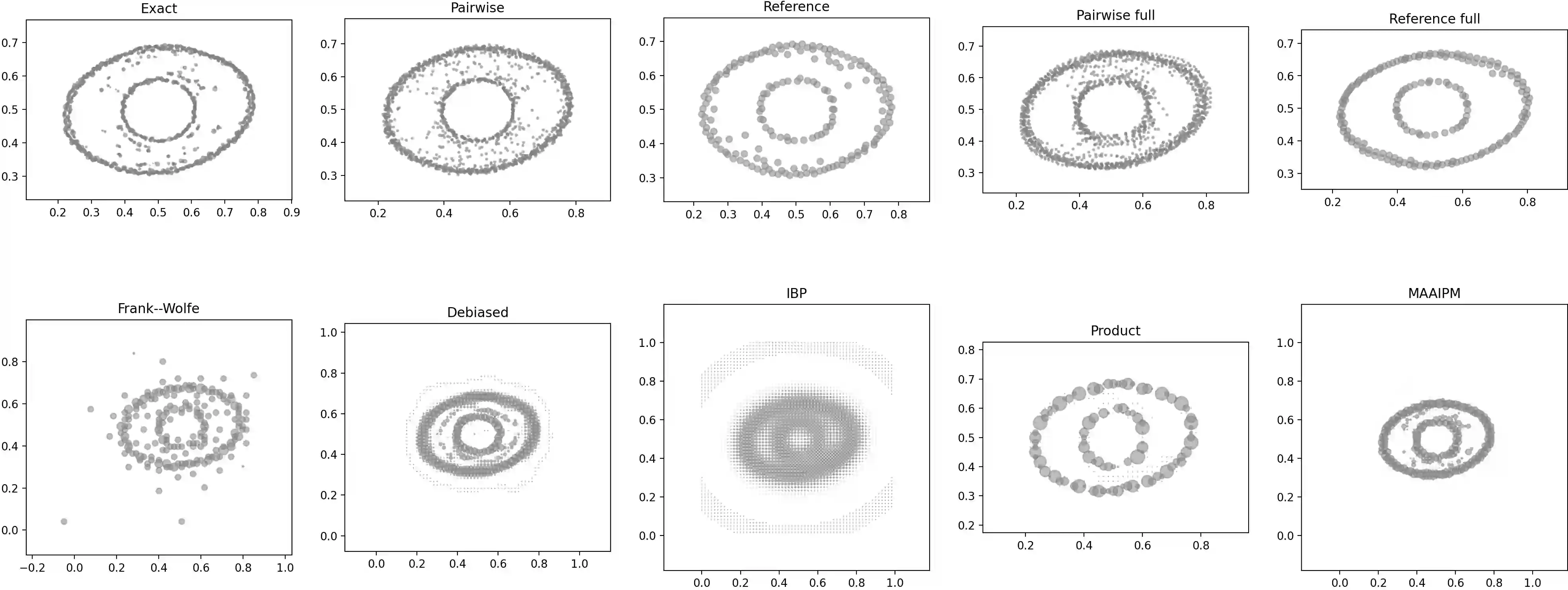
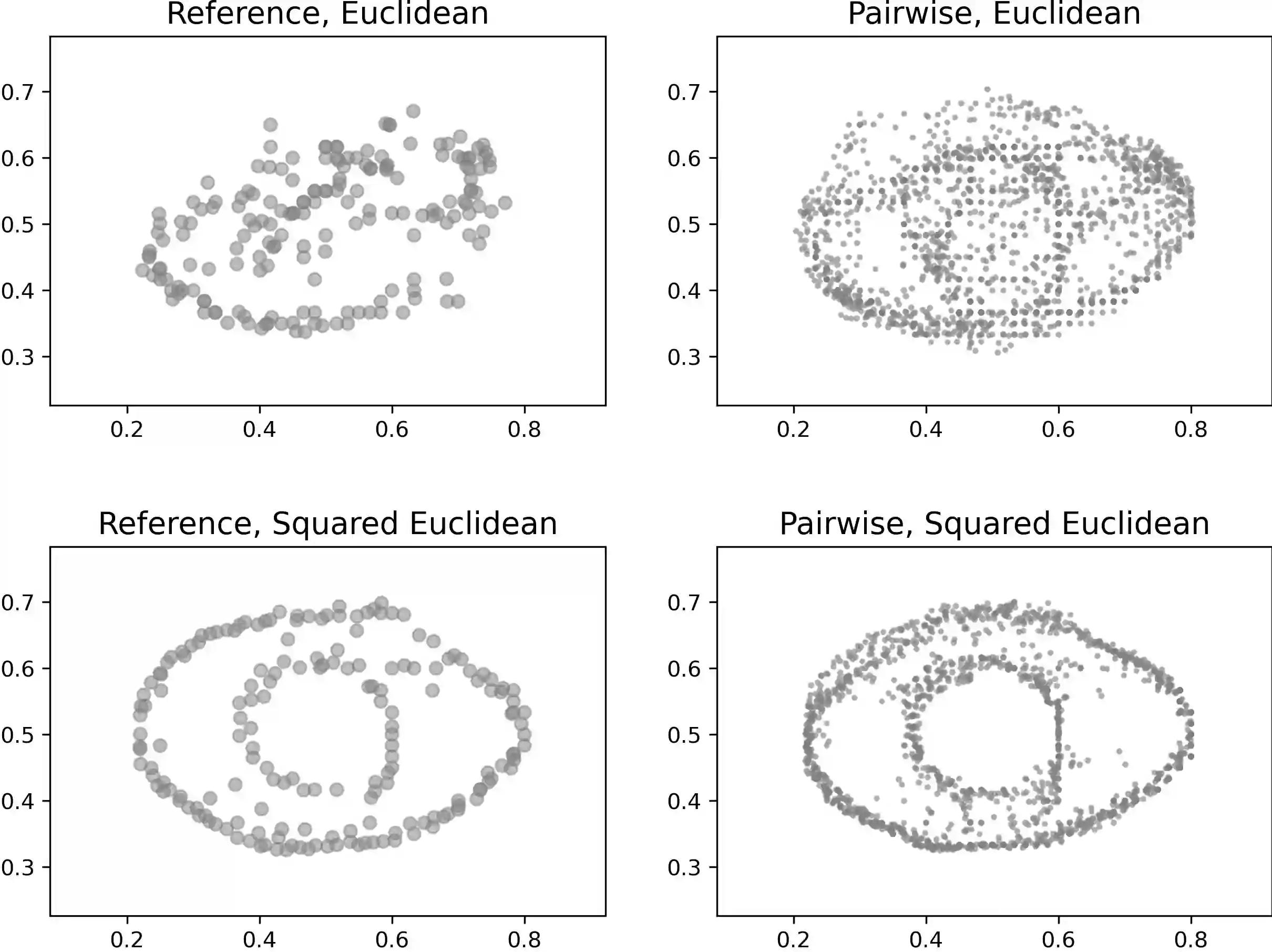
Computing Wasserstein barycenters of discrete measures has recently attracted considerable attention due to its wide variety of applications in data science. In general, this problem is NP-hard, calling for practical approximative algorithms. In this paper, we analyze a well-known simple framework for approximating Wasserstein-$p$ barycenters, where we mainly consider the most common case $p=2$ and $p=1$, which is not as well discussed. The framework produces sparse support solutions and shows good numerical results in the free-support setting. Depending on the desired level of accuracy, this requires only $N-1$ or $N(N-1)/2$ standard two-marginal optimal transport (OT) computations between the $N$ input measures, respectively, which is fast, memory-efficient and easy to implement using any OT solver as a black box. What is more, these methods yield a relative error of at most $N$ and $2$, respectively, for both $p=1, 2$. We show that these bounds are practically sharp. In light of the hardness of the problem, it is not surprising that such guarantees cannot be close to optimality in general. Nevertheless, these error bounds usually turn out to be drastically lower for a given particular problem in practice and can be evaluated with almost no computational overhead, in particular without knowledge of the optimal solution. In our numerical experiments, this guaranteed errors of at most a few percent.
翻译:由于数据科学的应用种类繁多,离散措施的瓦塞斯坦分流器最近引起了相当的关注。 一般来说, 这个问题是NP- 硬的, 需要实际的近似算法。 在本文中, 我们分析一个众所周知的简单框架, 用于接近瓦塞斯坦- $p$ 百分点, 我们主要将最常见的 $p=2美元和$p=1美元视为黑盒, 讨论得不够充分。 框架产生了稀少的支持解决方案, 并在自由支持设置中显示了良好的数字结果。 根据所期望的准确度, 这需要的只是N-1美元或$N( N-1/ 2美元) 标准双边最佳运输( OT), 这需要分别在 $n 的输入措施之间计算一个众所周知的简单框架, 这个框架是快速的, 记忆效率高, 并且容易使用任何 OT 解答器作为黑盒。 更重要的是, 这些方法产生一个相对的错误, 最多为$ $ 和 $2 美元, 美元, 在 免费支持设置的设置中, 。 我们显示这些界限实际上是精确的。 根据最接近精确的 的计算方法,, 在最接近的轨道中, 最精确的计算中, 通常不会被评估的问题是 。