Hypothesis testing for populations of networks

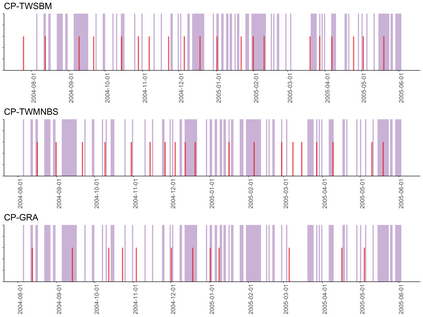
It has become an increasingly common practice for scientists in modern science and engineering to collect samples of multiple network data in which a network serves as a basic data object. The increasing prevalence of multiple network data calls for developments of models and theory that can deal with inference problems for populations of networks. In this work, we propose a general procedure for hypothesis testing of networks and in particular, for differentiating distributions of two samples of networks. We consider a very general framework which allows us to perform tests on large and sparse networks. Our contribution is two-fold: (1) We propose a test statistics based on the singular value of a generalized Wigner matrix. The asymptotic null distribution of the statistics is shown to follow the Tracy--Widom distribution as the number of nodes tends to infinity. The test also yields asymptotic power guarantee with the power tending to one under the alternative; (2) The test procedure is adapted for change-point detection in dynamic networks which is proven to be consistent in detecting the change-points. In addition to theoretical guarantees, another appealing feature of this adapted procedure is that it provides a principled and simple method for selecting the threshold that is also allowed to vary with time. Extensive simulation studies and real data analyses demonstrate the superior performance of our procedure with competitors.