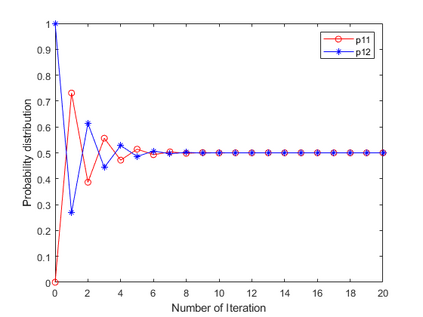
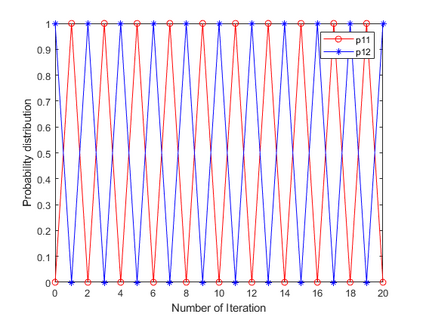
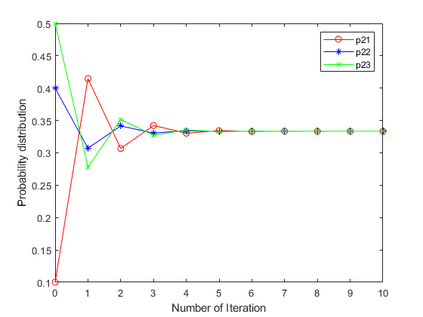
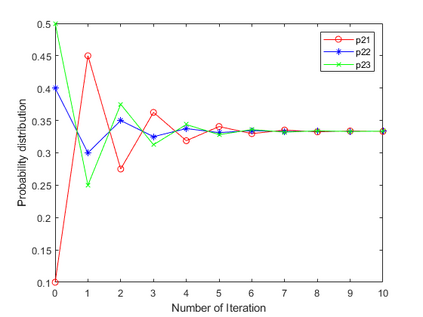
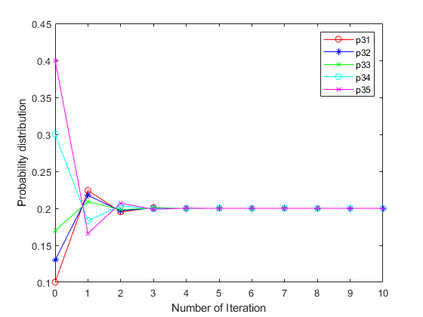
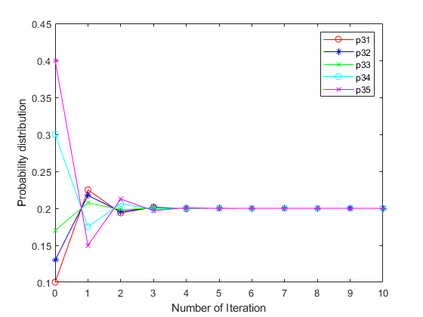
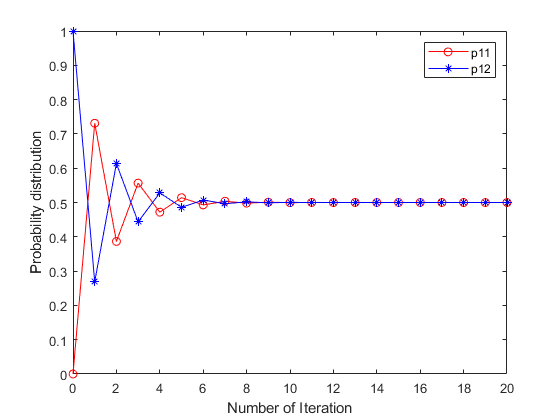
Negation operation is important in intelligent information processing. Different with existing arithmetic negation, an exponential negation is presented in this paper. The new negation can be seen as a kind of geometry negation. Some basic properties of the proposed negation is investigated, we find that the fix point is the uniform probability distribution. The negation is an entropy increase operation and all the probability distributions will converge to the uniform distribution after multiple negation iterations. The number of iterations of convergence is inversely proportional to the number of elements in the distribution. Some numerical examples are used to illustrate the efficiency of the proposed negation.
翻译:偏差操作在智能信息处理中很重要。 与现有的算术否定不同, 本文中呈现了指数否定。 新的否定可以被视为一种几何否定。 对拟议的否定的某些基本特性进行了调查, 我们发现, 确定点是统一概率分布。 否定是一个增生操作, 所有概率分布都会在多次否定重复后会汇合到统一分布中。 趋同的迭代数与分布中元素数量成反比。 一些数字例子用来说明提议的否定的效率 。