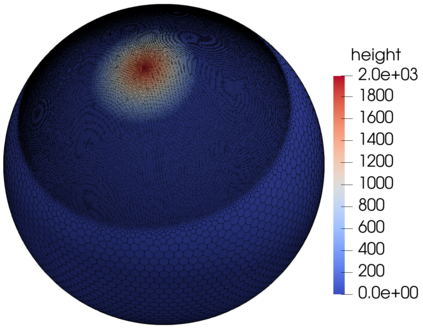
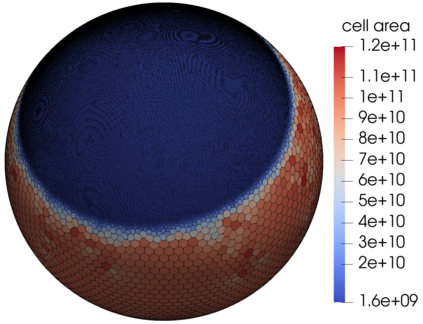
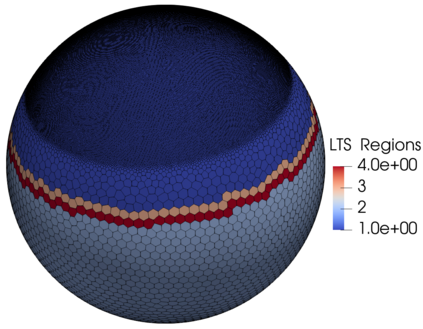
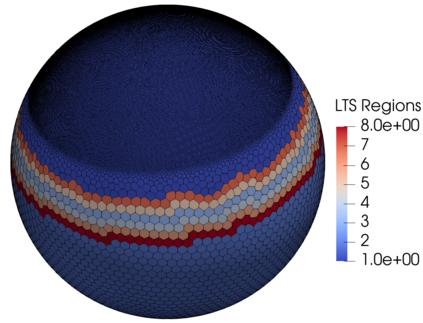
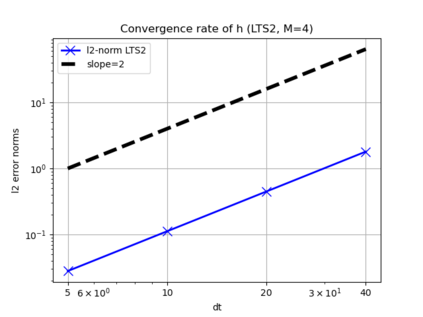
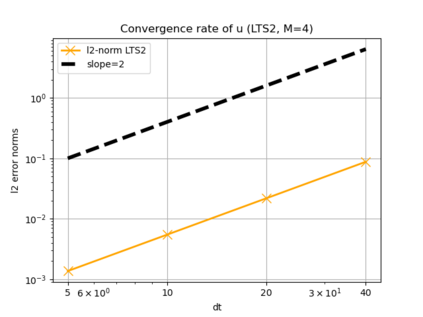
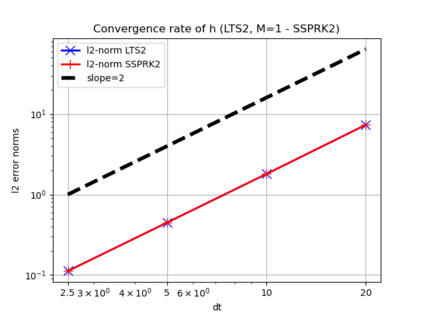
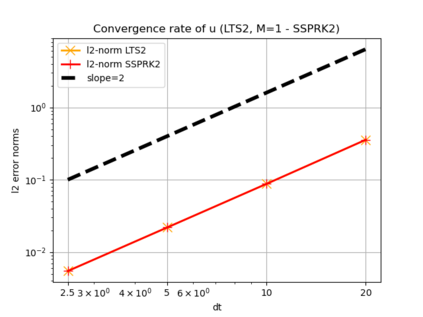
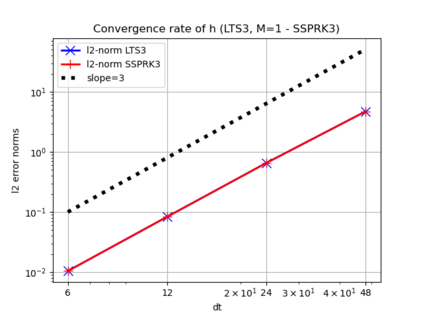
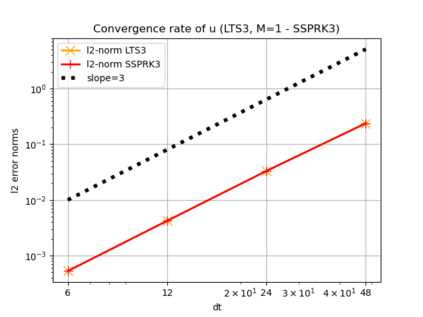
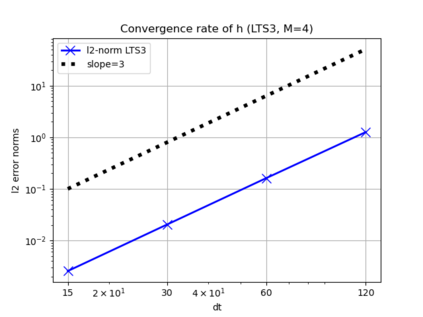
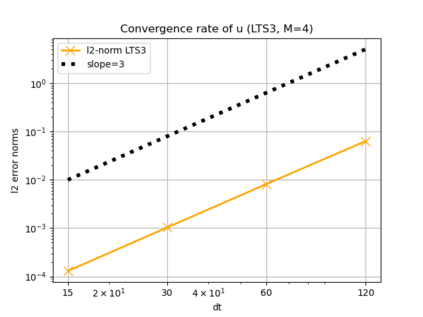
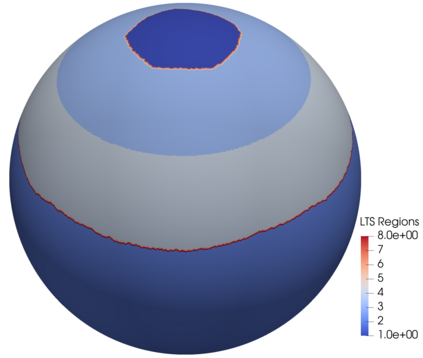
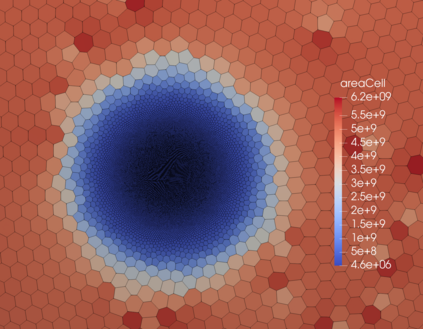
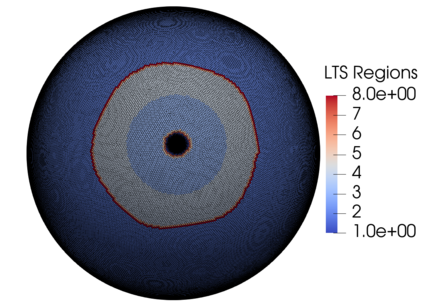
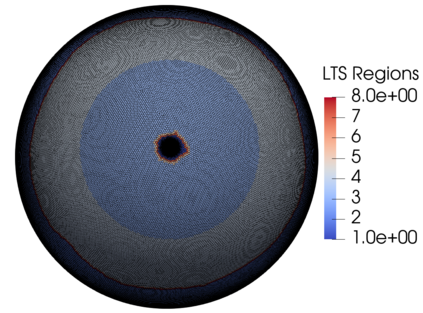
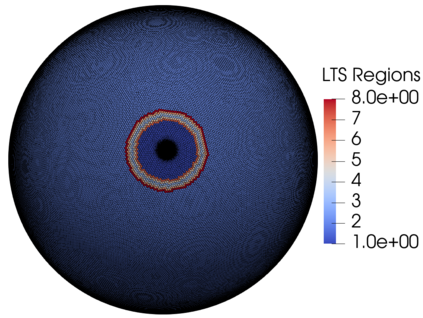
We assess the performance of a set of local time-stepping (LTS) schemes for the shallow water equations implemented in the Model for Prediction Across Scales (MPAS). The goal of LTS is to speed up the simulation by allowing different time-steps on different regions of the computational grid. The LTS schemes considered here were originally introduced by Hoang et al. (J. Comput. Phys., Vol. 382, p.152-176, 2019), who laid out the mathematical foundation of the methods. Here, the authors take on the task of presenting a fast, efficient and scalable parallel implementation of these LTS methods on high performance computing machines, with the aim to provide a recipe for other climate modeling groups that may be interested in employing LTS algorithms in their codes. As a matter of fact, even if MPAS is our framework of choice, our approach is general enough and could be of interest to other groups beyond the MPAS community. Due to their nature, LTS methods possess an inherent load imbalance that needs to be carefully addressed in order to obtain efficient scalability. Even more important is the far from trivial task of computing the right-hand side terms only on specific LTS regions during the time-stepping procedure. An inefficient handling of this task causes a drastic decay of the CPU time performance, making the LTS algorithms practically of no use. The emphasis of the present work is therefore on the computational and parallel aspects of the LTS methods, whose proper handling is crucial to make the methods run faster against existing strategies, such as for instance high-order explicit global time-stepping schemes. This is in fact the ultimate goal of using an LTS procedure and it is the one to which we direct all our optimization efforts.
翻译:我们评估了在《全局预测模型》中实施的一套浅水方程式当地时间步(LTS)的绩效。 LTS的目标是通过在计算网的不同区域允许不同的时间步来加快模拟。这里考虑的LTS计划最初是由Hoang等人提出的(J.Compuut.Phys.,vol.382,p.152-176,2019),他们为方法奠定了数学基础。在这里,作者承担的任务是在高性能计算机器上快速、高效和可扩展地平行实施LTS方法,目的是为其他气候模型组提供一种配方,这些模型组可能有兴趣在计算网格的不同区域采用LTS算法。事实上,即使MPAS是我们的选择框架,我们的方法已经很笼统,而且可能对MPAS社区以外的其他群体感兴趣。LTS方法具有内在的负荷不平衡性,为了获得高效的可调和可伸缩性,我们在处理高性计算高性计算机操作程序时,更需要小心地处理LTS过程的正确速度,因此,在最短的轨道上,在计算最短的轨道上要紧的轨道上,这是一个最短的轨道上,在最短的轨道上,在最短的轨道上要的轨道上,在计算一个最短的轨道上,在最短的轨道上,也就是的轨道上,在计算一个最短的轨道上,也就是的轨道上,在计算一个过程是,在目前的工作程序是,在最短的轨道上,在最短的轨道上进行。