Tree stick-breaking priors for covariate-dependent mixture models

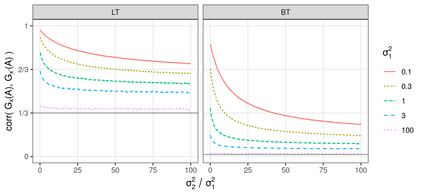
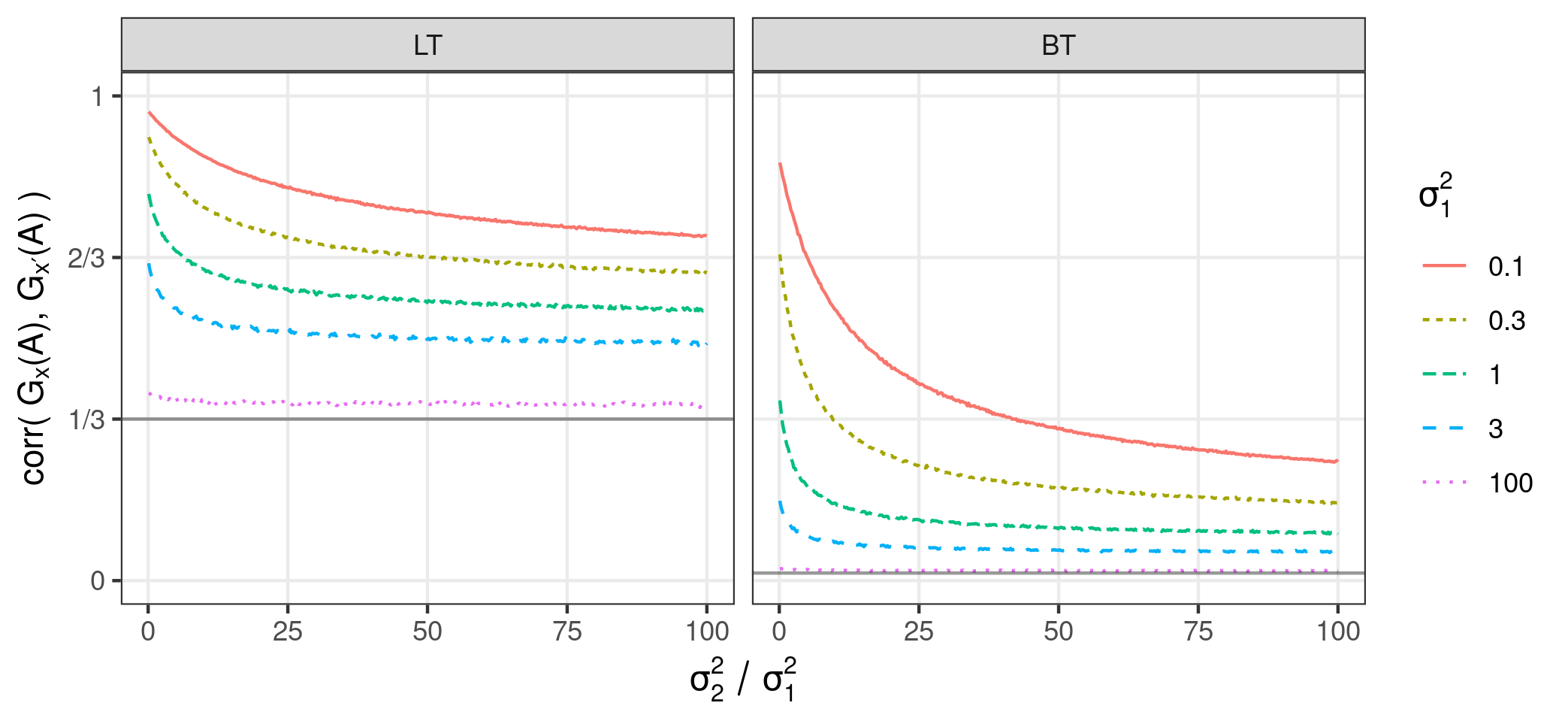
Stick-breaking priors are often adopted in Bayesian nonparametric mixture models for generating mixing weights. When covariates influence the sizes of clusters, stick-breaking mixtures can leverage various computational techniques for binary regression to ease posterior computation. Existing stick-breaking priors are typically based on continually breaking a single remaining piece of the unit stick. We demonstrate that this ``single-piece'' scheme can induce three highly undesirable behaviors; these behaviors are circumvented by our proposed model which continually breaks off all remaining pieces of a unit stick while keeping posterior computation essentially identical. Specifically, the new model provides more flexibility in setting cross-covariate prior correlation among the generated random measures, mitigates the impact of component label switching when posterior simulation is performed using Markov chain Monte Carlo, and removes the imposed artificial decay of posterior uncertainty on the mixing weights according to when the weight is ``broken off'' the unit stick. Unlike previous works on covariate-dependent mixtures, which focus on estimating covariate-dependent distributions, we instead focus on inferring the effects of individual covariates on the mixture weights in a fashion similar to classical regression analysis, and propose a new class of posterior predictives for summarizing covariate effects.