To Bag is to Prune

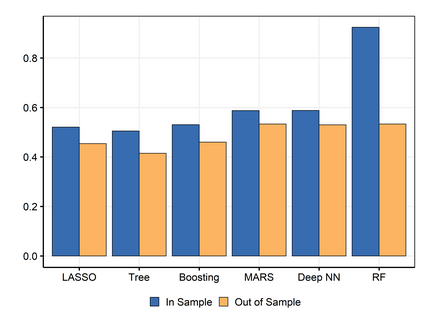
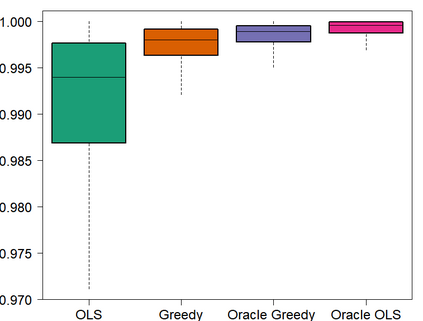
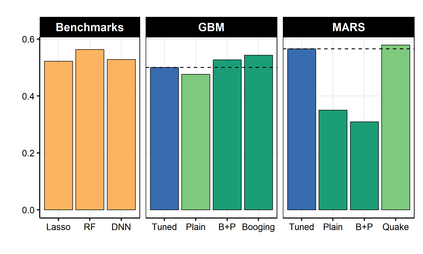
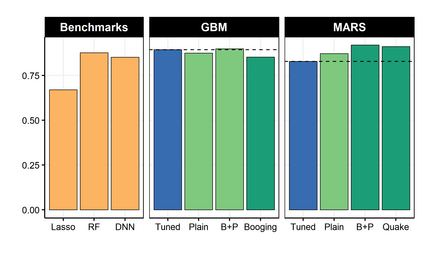
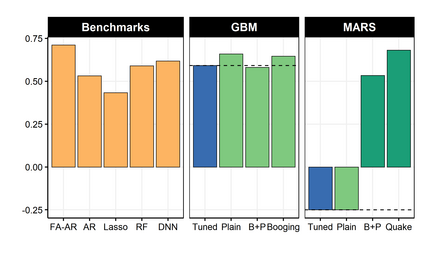
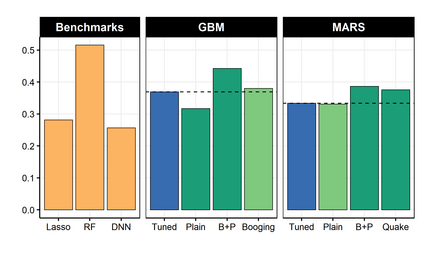
It is notoriously difficult to build a bad Random Forest (RF). Concurrently, RF is perhaps the only standard ML algorithm that blatantly overfits in-sample without any consequence out-of-sample. Standard arguments cannot rationalize this paradox. I propose a new explanation: bootstrap aggregation and model perturbation as implemented by RF automatically prune a (latent) true underlying tree. More generally, randomized ensembles of greedily optimized learners implicitly perform optimal early stopping out-of-sample. So there is no need to tune the stopping point. By construction, variants of Boosting and MARS are also eligible for automatic tuning. I empirically demonstrate the property, with simulated and real data, by reporting that these new completely overfitting ensembles yield an out-of-sample performance equivalent to that of their tuned counterparts -- or better.