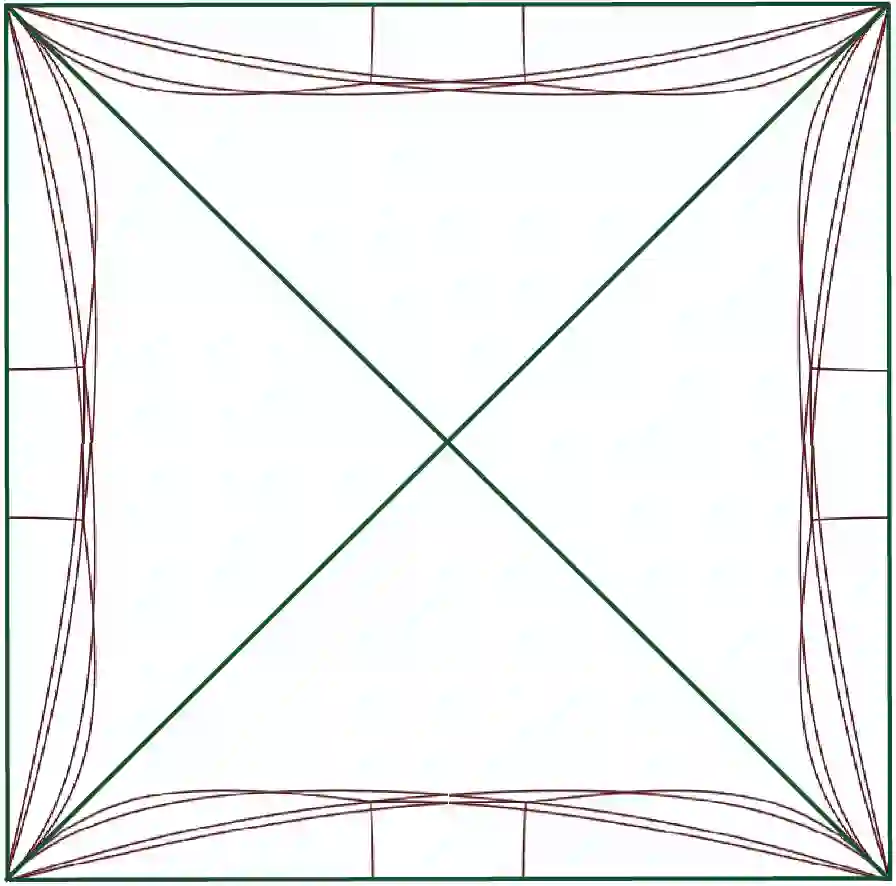
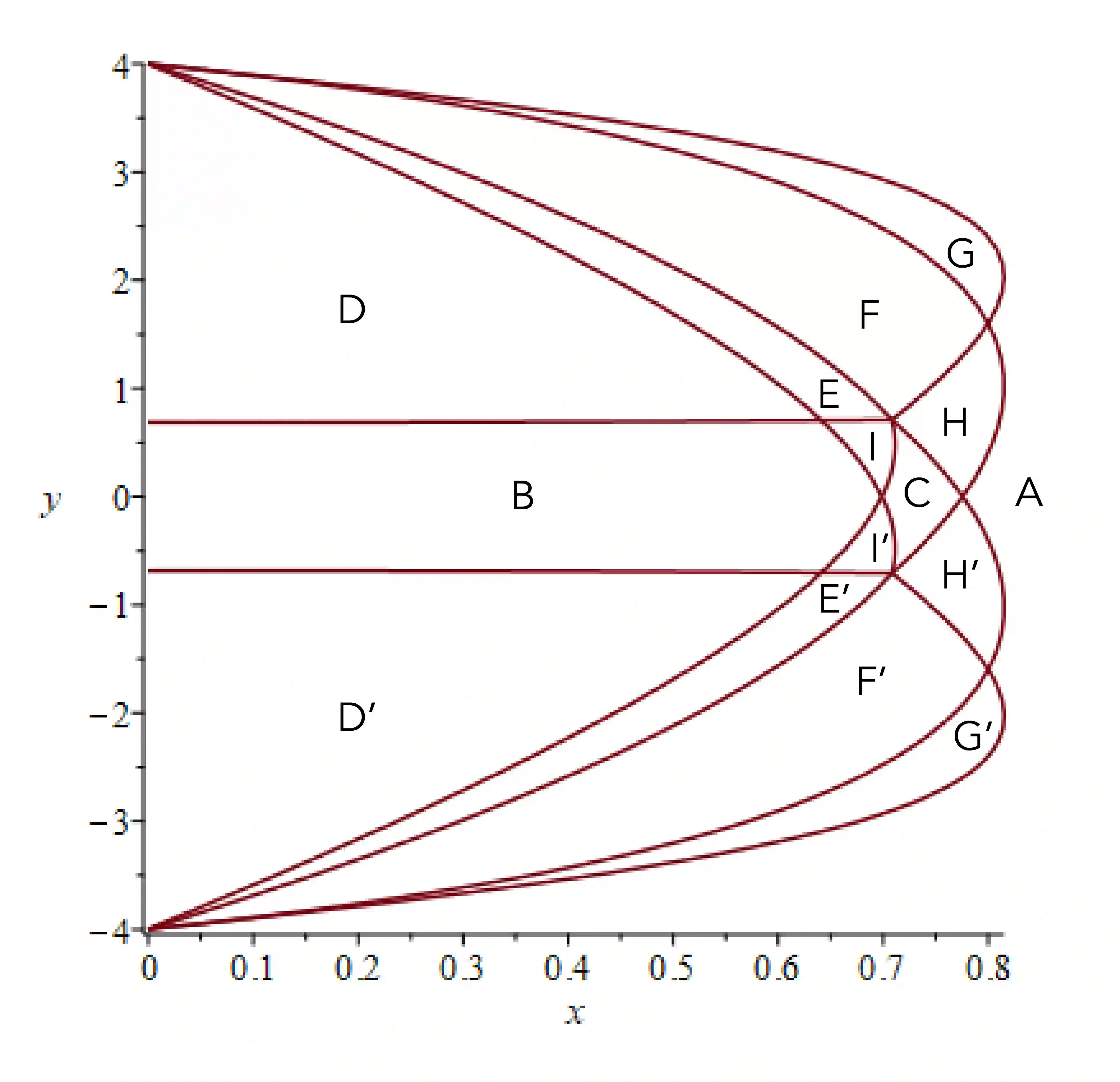
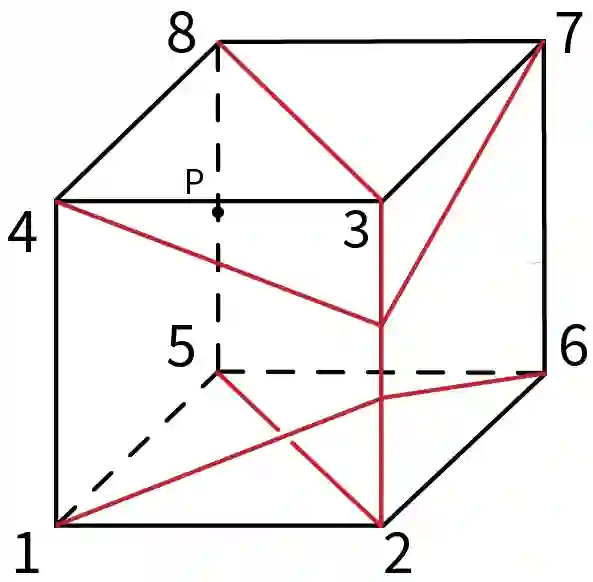
The topological (resp. geodesic) complexity of a topological (resp. metric) space is roughly the smallest number of continuous rules required to choose paths (resp. shortest paths) between any points of the space. We prove that the geodesic complexity of a cube exceeds its topological complexity by exactly 2. The proof involves a careful analysis of cut loci of the cube.
翻译：暂无翻译
相关内容
让 iOS 8 和 OS X Yosemite 无缝切换的一个新特性。
> Apple products have always been designed to work together beautifully. But now they may really surprise you. With iOS 8 and OS X Yosemite, you’ll be able to do more wonderful things than ever before.
Source: Apple - iOS 8
Source: Apple - iOS 8
专知会员服务
29+阅读 · 2019年10月18日
专知会员服务
34+阅读 · 2019年10月17日
Arxiv
0+阅读 · 2023年9月28日
相关主题
相关VIP内容
专知会员服务
29+阅读 · 2019年10月18日
专知会员服务
34+阅读 · 2019年10月17日
相关资讯
微信扫码咨询专知VIP会员