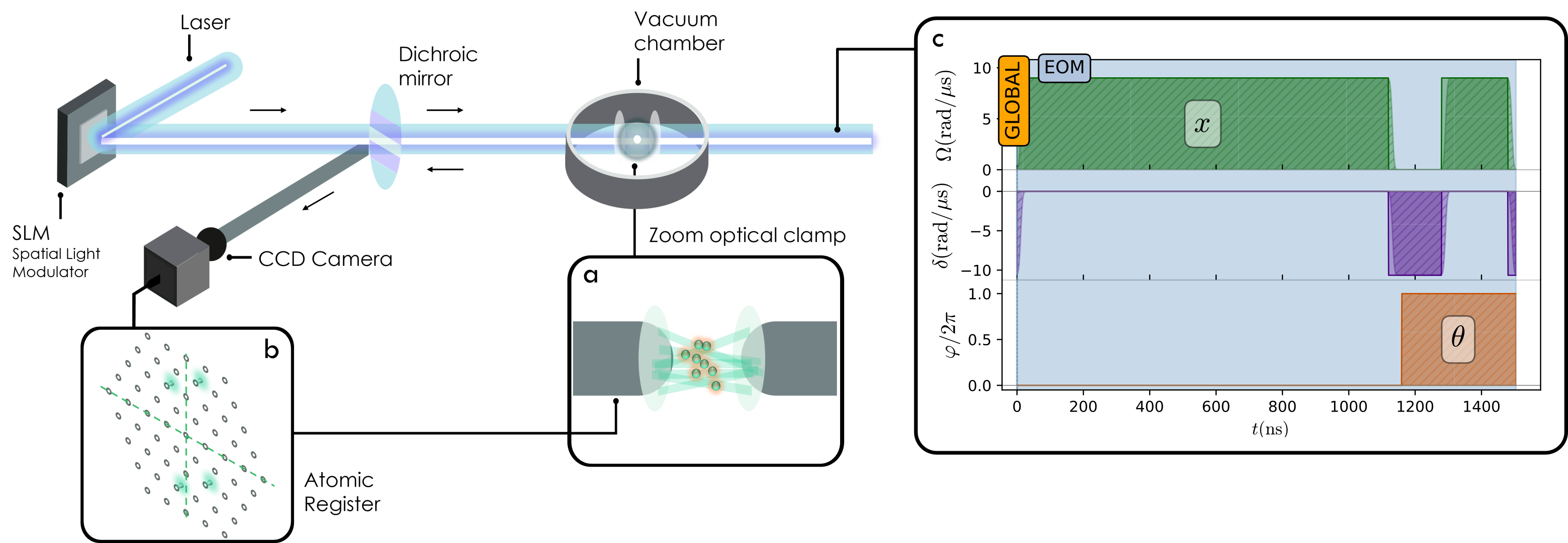
Solving and optimizing differential equations (DEs) is ubiquitous in both engineering and fundamental science. The promise of quantum architectures to accelerate scientific computing thus naturally involved interest towards how efficiently quantum algorithms can solve DEs. Differentiable quantum circuits (DQC) offer a viable route to compute DE solutions using a variational approach amenable to existing quantum computers, by producing a machine-learnable surrogate of the solution. Quantum extremal learning (QEL) complements such approach by finding extreme points in the output of learnable models of unknown (implicit) functions, offering a powerful tool to bypass a full DE solution, in cases where the crux consists in retrieving solution extrema. In this work, we provide the results from the first experimental demonstration of both DQC and QEL, displaying their performance on a synthetic usecase. Whilst both DQC and QEL are expected to require digital quantum hardware, we successfully challenge this assumption by running a closed-loop instance on a commercial analog quantum computer, based upon neutral atom technology.
翻译:暂无翻译