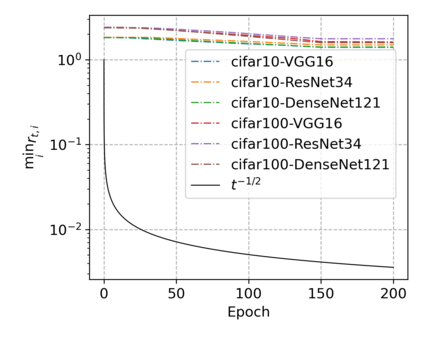
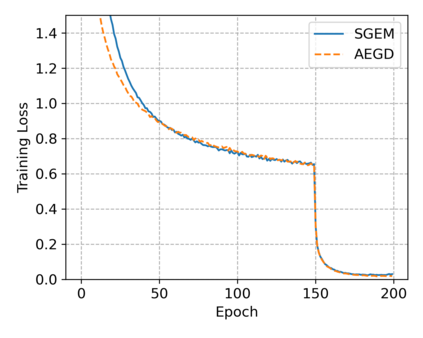
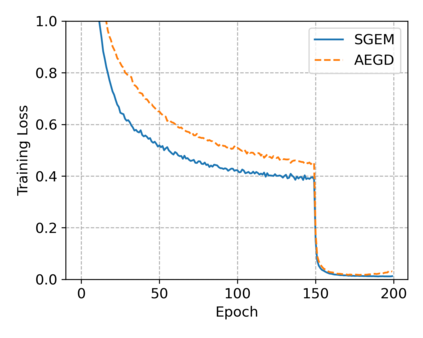
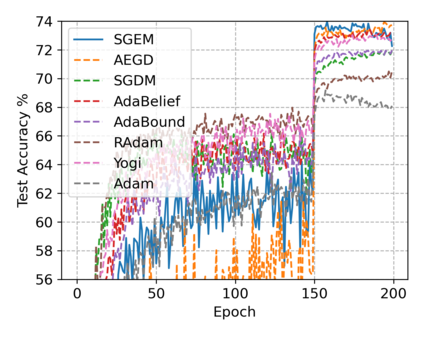
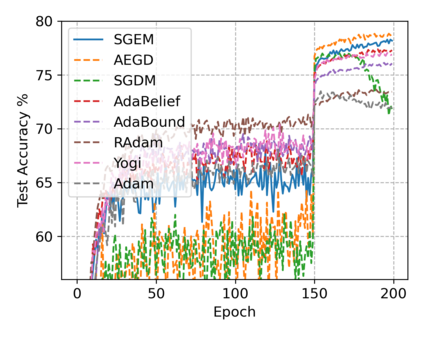
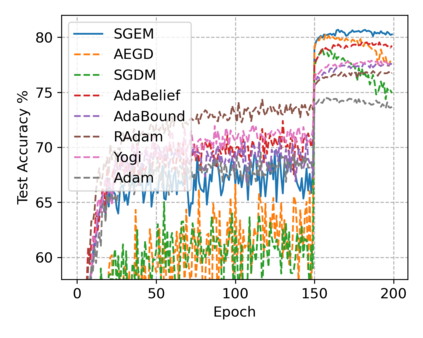
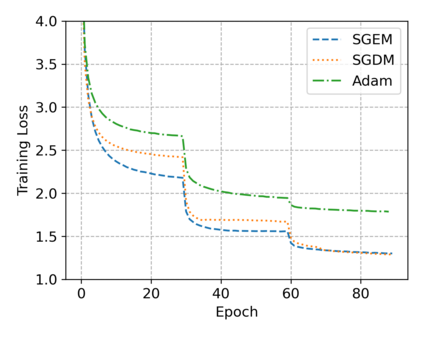
In this paper, we propose SGEM, Stochastic Gradient with Energy and Momentum, to solve a large class of general non-convex stochastic optimization problems, based on the AEGD method that originated in the work [AEGD: Adaptive Gradient Descent with Energy. arXiv: 2010.05109]. SGEM incorporates both energy and momentum at the same time so as to inherit their dual advantages. We show that SGEM features an unconditional energy stability property, and derive energy-dependent convergence rates in the general nonconvex stochastic setting, as well as a regret bound in the online convex setting. A lower threshold for the energy variable is also provided. Our experimental results show that SGEM converges faster than AEGD and generalizes better or at least as well as SGDM in training some deep neural networks.
翻译:在本文中,我们建议SGEM, " 与能量和动力的蒸汽梯度梯度梯度梯度梯度梯度梯度梯度梯度 ",以基于工作[AEGD:与能量相适应的梯度梯度梯度梯度[AEGD:与能量相适应的梯度梯度梯度梯度梯度梯度:2010/05109]的AEGD方法为基础,解决一大批一般的非凝固性非凝固性优化问题。SSGEM同时结合了能量和动力,以继承其双重优势。我们表明SGEM具有无条件的能源稳定性特性,在一般的非凝固性定位中得出了依赖能源的趋同率,并在在线凝固器设置中得出了遗憾。还提供了能源变量下限。我们的实验结果表明,SGEM比AEGD更快地结合,在培训一些深层神经网络时,总化或至少是SGDMM的更好或更普遍化。