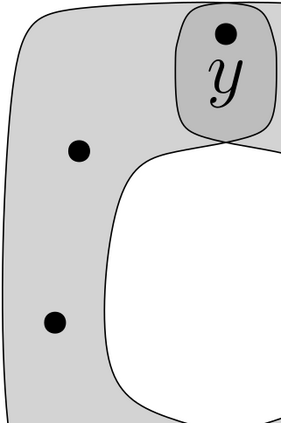
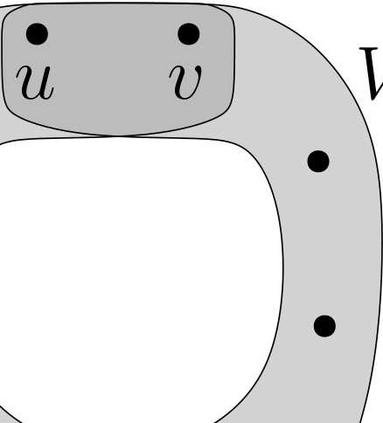
In the Maker-Breaker positional game, Maker and Breaker take turns picking vertices of a hypergraph $H$, and Maker wins if and only if he claims all the vertices of some edge of $H$. This paper provides a general framework to study Maker-Breaker games, centered on the notion of danger at a vertex $x$, which is a subhypergraph representing an urgent threat that Breaker must hit with his next pick if Maker picks $x$. We then apply this concept in hypergraphs of rank 3, providing a structural characterization of the winner with perfect play as well as optimal strategies for both players based on danger intersections. We construct a family $\mathcal{F}$ of dangers such that a hypergraph $H$ of rank 3 is a Breaker win if and only if the $\mathcal{F}$-dangers at $x$ in $H$ intersect for all $x$. By construction of $\mathcal{F}$, this will mean that $H$ is a Maker win if and only if Maker can guarantee the appearance, within the first three rounds of play, of a very specific elementary subhypergraph (on which Maker easily wins). This last result has a consequence on the algorithmic complexity of deciding which player has a winning strategy on a given hypergraph: this problem, which is known to be PSPACE-complete on 6-uniform hypergraphs, is in polynomial time on hypergraphs of rank 3. This validates a conjecture by Rahman and Watson. Another corollary of our result is that, if Maker has a winning strategy on a hypergraph of rank 3, then he can ensure to claim an edge in a number of rounds that is logarithmic in the number of vertices. Note: The present updated version of this deposit provides a counterexample to a similar result which was incorrectly claimed recently (arXiv:2209.11202).
翻译:在Maker-Breaker 定位游戏中, Maker 和 Breaker 轮流摘取高压的脊椎 $H美元,而Maker 只有在他声称某些边缘的所有脊椎为$H美元的情况下,Maker 和 Breaker 才会赢。本文提供了一个研究Maker-Breaker 游戏的一般框架,其中心是在一个顶点$x美元上的危险概念,这是Breader如果Maker 选取$22美元,就必须用下一个选择来打击一个紧急威胁。我们然后在3级高压中应用这个概念,为赢者提供完美的游戏结构特征,以及基于危险交叉点的两种玩家的最佳策略。我们建造了一个家庭 $mathcal{Fr, 3级高压$Heworm 是一个突破点的胜利, 只有在 $mathalcal logal ibreal ial ibloral 时, 才能在6Hax ial ial ial ial ial 上提出这个结果。