Cross-Population Amplitude Coupling in High-Dimensional Oscillatory Neural Time Series

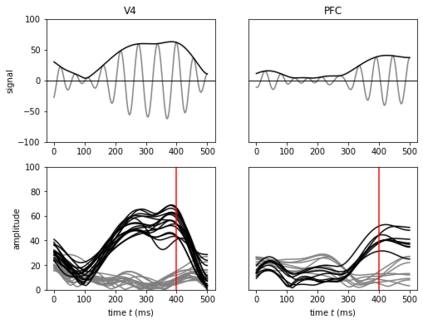
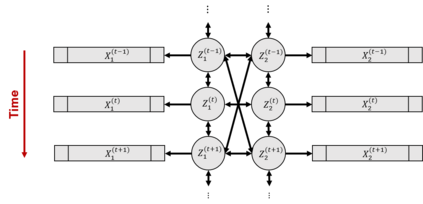
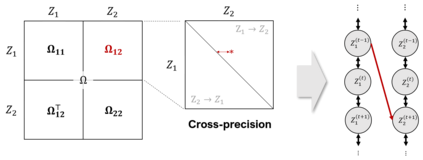
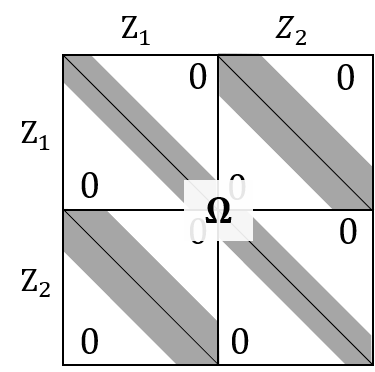
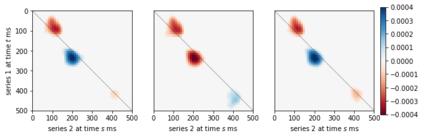
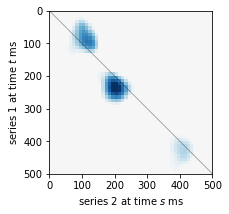
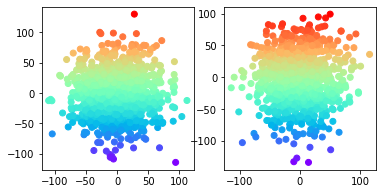
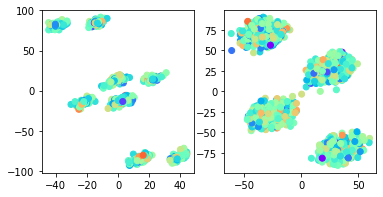
An important outstanding problem in analysis of neural data is to characterize interactions across brain regions from high-dimensional multiple-electrode recordings during a behavioral experiment. A leading theory, based on a considerable body of research, is that oscillations represent coordinated activity across populations of neurons. We sought to quantify time-varying covariation of oscillatory amplitudes across two brain regions, during a memory task, based on neural potentials recorded from 96 electrodes in each region. We extended probabilistic Canonical Correlation Analysis (CCA) to the time series setting, which provides a new interpretation of multiset CCA based on cross-correlation of latent time series. Because the latent time series covariance matrix is high-dimensional, we assumed sparsity of partial correlations within a range of possible interesting time series lead-lag effects to derive procedures for estimation and inference. We found the resulting methodology to perform well in realistic settings, and we applied it to data recorded from prefrontal cortex and visual area V4 to produce results that are highly plausible based on existing literature.